Exam 3: Limits and Continuity
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
For the function f whose graph is given, determine the limit.
-
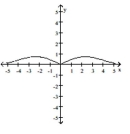
(Multiple Choice)
4.8/5  (40)
(40)
Provide an appropriate response.
-Suppose and . Name the limit rules that are used to accomplish steps (a), (b), and (c) of the following calculation.
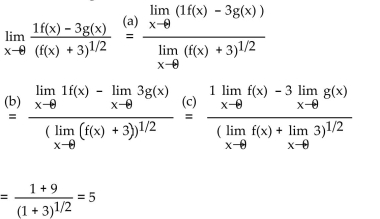
(Multiple Choice)
4.9/5  (35)
(35)
Provide an appropriate response.
-It can be shown that the inequalities hold for all values of . Find if it exists.
(Multiple Choice)
5.0/5  (33)
(33)
Solve the problem.
-The cross-sectional area of a cylinder is given by , where is the cylinder diameter. Find the tolerance range of such that as long as .
(Multiple Choice)
4.9/5  (35)
(35)
Provide an appropriate response.
-If and is an odd function, which of the following statements are true?
I.
II.
III. does not exist.
(Multiple Choice)
4.8/5  (35)
(35)
Graph the rational function. Include the graphs and equations of the asymptotes.
-
(Multiple Choice)
4.7/5  (38)
(38)
Use a CAS to plot the function near the point x0 being approached. From your plot guess the value of the limit.
-
(Multiple Choice)
4.8/5  (34)
(34)
Find the limit and determine if the function is continuous at the point being approached.
-
(Multiple Choice)
4.9/5  (32)
(32)
Solve the problem.
-
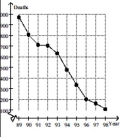 Estimate the average rate of change in tuberculosis deaths from 1996 to 1998.
Estimate the average rate of change in tuberculosis deaths from 1996 to 1998.
(Multiple Choice)
4.9/5  (36)
(36)
Use the table of values of f to estimate the limit.
-
1.9 1.99 1.999 2.001 2.01 2.1 ()
(Multiple Choice)
4.7/5  (42)
(42)
Graph the rational function. Include the graphs and equations of the asymptotes.
-
(Multiple Choice)
4.9/5  (39)
(39)
Solve the problem.
-The current in a simple electrical circuit is given by , where is the current in amperes, is the voltage in volts, and is the resistance in ohms. When volts, what is a resistor's tolerance for the current to be within amp?
(Multiple Choice)
4.8/5  (45)
(45)
Solve the problem.
-To what new value should be changed to remove the discontinuity?
(Multiple Choice)
4.8/5  (34)
(34)
Showing 301 - 320 of 327
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)