Exam 3: Limits and Continuity
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
Use a CAS to plot the function near the point x0 being approached. From your plot guess the value of the limit.
-
(Multiple Choice)
4.9/5  (40)
(40)
For the function f whose graph is given, determine the limit.
-Find .
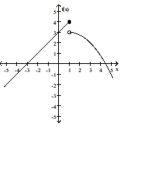
(Multiple Choice)
4.8/5  (35)
(35)
Find the average rate of change of the function over the given interval.
-
(Multiple Choice)
4.7/5  (33)
(33)
Use the table to estimate the rate of change of y at the specified value of x.
-
x 0 0 .2 0.02 .4 0.08 .6 0.18 .8 0.32 0 0.5 .2 0.72 .4 0.98
(Multiple Choice)
4.8/5  (33)
(33)
Determine if the given function can be extended to a continuous function at x = 0. If so, approximate the extended
function's value at x = 0 (rounded to four decimal places if necessary). If not, determine whether the function can be
continuously extended from the left or from the right and provide the values of the extended functions at x = 0.
Otherwise write "no continuous extension."
-
(Multiple Choice)
4.8/5  (44)
(44)
Showing 61 - 80 of 327
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)