Exam 3: Limits and Continuity
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
Provide an appropriate response.
-Give an example of a function f(x) that is continuous for all values of x except x = 10, where it has a
nonremovable discontinuity. Explain how you know that f is discontinuous at x = 10 and why the discontinuity
is nonremovable.
(Essay)
4.8/5  (40)
(40)
For the function f whose graph is given, determine the limit.
-
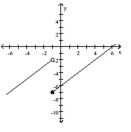
(Multiple Choice)
4.8/5  (37)
(37)
Sketch the graph of a function y = f(x) that satisfies the given conditions.
-
(Essay)
4.8/5  (44)
(44)
A function , a point , the limit of as approaches , and a positive number is given. Find a number such that for all .
- , and
(Multiple Choice)
4.7/5  (42)
(42)
Use the slopes of UQ, UR, US, and UT to estimate the rate of change of y at the specified value of x.
-

(Multiple Choice)
5.0/5  (36)
(36)
Divide numerator and denominator by the highest power of x in the denominator to find the limit.
-
(Multiple Choice)
4.9/5  (38)
(38)
Use a CAS to plot the function near the point x0 being approached. From your plot guess the value of the limit.
-What conditions, when present, are sufficient to conclude that a function has a limit as approaches some value of a?
(Multiple Choice)
4.7/5  (39)
(39)
A function , a point , the limit of as approaches , and a positive number is given. Find a number such that for all .
-
(Multiple Choice)
4.8/5  (41)
(41)
Provide an appropriate response.
-If , which of the following expressions are true?
I. does not exist.
II. does not exist.
III.
IV.
(Multiple Choice)
4.9/5  (32)
(32)
Use a CAS to plot the function near the point x0 being approached. From your plot guess the value of the limit.
-
(Multiple Choice)
4.9/5  (42)
(42)
Find numbers a and b, or k, so that f is continuous at every point.
-
(Multiple Choice)
4.8/5  (40)
(40)
Divide numerator and denominator by the highest power of x in the denominator to find the limit.
-
(Multiple Choice)
4.8/5  (30)
(30)
Showing 141 - 160 of 327
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)