Exam 17: Integrals and Vector Fields
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
Evaluate the line integral along the curve C.
- is the curve
(Multiple Choice)
4.9/5  (43)
(43)
Solve the problem.
-The shape and density of a thin shell are indicated below. Find the moment of inertia about the -axis. Shell: upper hemisphere of cut by the plane Density:
(Multiple Choice)
4.8/5  (38)
(38)
Calculate the area of the surface S.
- is the lower portion of the sphere cut by the cone .
(Multiple Choice)
4.8/5  (39)
(39)
Solve the problem.
-The radial flow field of an incompressible fluid is shown below. For which of the closed paths is the circulation not necessarily zero?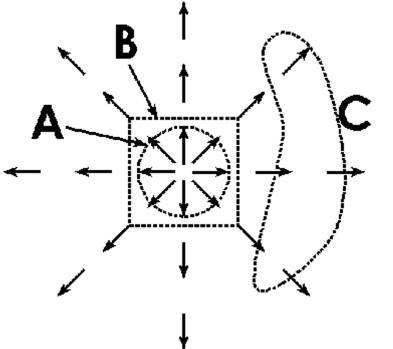
(Multiple Choice)
4.8/5  (43)
(43)
Solve the problem.
-Imagine a force field in which the force is always perpendicular to dr. What is special about the work done in
moving a particle in such a field?
(Short Answer)
4.8/5  (42)
(42)
Calculate the flux of the field F across the closed plane curve C.
- the curve is the counterclockwise path around the circle
(Multiple Choice)
4.9/5  (40)
(40)
Find the equation for the plane tangent to the parametrized surface S at the point P.
-
(Essay)
4.9/5  (42)
(42)
Test the vector field F to determine if it is conservative.
-
(Multiple Choice)
4.8/5  (43)
(43)
Find the flux of the vector field F across the surface S in the indicated direction.
- is the cap cut from the sphere by the plane , direction is outward
(Multiple Choice)
4.8/5  (36)
(36)
Find the work done by F over the curve in the direction of increasing t.
-
(Multiple Choice)
4.8/5  (32)
(32)
Find the surface area of the surface S.
- is the intersection of the plane and the cylinder with sides and .
(Multiple Choice)
4.7/5  (44)
(44)
Using Green's Theorem, compute the counterclockwise circulation of F around the closed curve C.
- is the lobe of the lemniscate that lies in the first quadrant.
(Multiple Choice)
4.7/5  (38)
(38)
Solve the problem.
-In thermodynamics, the differential form of the internal energy of a system is , where is the internal energy, is the temperature, is the entropy, is the pressure, and is the volume of the system. The First Law of Thermodynamics asserts that dU is an exact differential. Using this information, justify the thermodynamic relation .
(Essay)
4.7/5  (41)
(41)
Showing 81 - 100 of 277
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)