Exam 17: Integrals and Vector Fields
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
Solve the problem.
-The radial flow field of an incompressible fluid is shown below. Which of the closed paths would exhibit a non-zero flux?
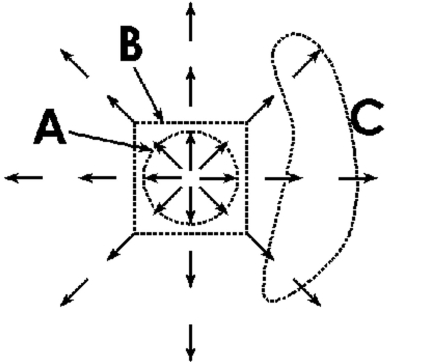
(Multiple Choice)
4.8/5  (37)
(37)
Using Green's Theorem, calculate the area of the indicated region.
-The circle
(Multiple Choice)
4.8/5  (35)
(35)
Find the equation for the plane tangent to the parametrized surface S at the point P.
-
(Essay)
4.7/5  (35)
(35)
Evaluate the surface integral of the function g over the surface S.
- is the surface of the rectangular prism formed from the coordinate planes and the planes , and
(Multiple Choice)
4.9/5  (34)
(34)
Test the vector field F to determine if it is conservative.
-F = xyi + yj + zk
(Multiple Choice)
4.8/5  (31)
(31)
Find the flux of the vector field F across the surface S in the indicated direction.
- ; is portion of the cone between and ; direction is outward
(Multiple Choice)
4.8/5  (44)
(44)
Solve the problem.
-The velocity field of a fluid is the spin field . Following the smooth curve from to , show that the flux across the curve is
(Essay)
4.8/5  (37)
(37)
Find the work done by F over the curve in the direction of increasing t.
-
(Multiple Choice)
4.9/5  (35)
(35)
Using the Divergence Theorem, find the outward flux of F across the boundary of the region D.
- ; D: the thick sphere
(Multiple Choice)
4.8/5  (33)
(33)
Find the flux of the curl of field F through the shell S.
-
(Multiple Choice)
4.8/5  (36)
(36)
Find the flux of the curl of field F through the shell S.
- is the upper hemisphere of
(Multiple Choice)
4.8/5  (37)
(37)
Using Green's Theorem, find the outward flux of F across the closed curve C.
-F = (x - y)i + (x + y)j; C is the triangle with vertices at (0, 0), (9, 0), and (0, 9)
(Multiple Choice)
4.8/5  (42)
(42)
Evaluate the surface integral of the function g over the surface S.
-G(x, y, z) = x + z; S is the surface of the wedge formed from the coordinate planes and the planes x + z = 3 and y = 5
(Multiple Choice)
4.8/5  (29)
(29)
Find the surface area of the surface S.
-S is the area cut from the plane by the cylinder .
(Multiple Choice)
4.8/5  (37)
(37)
Showing 41 - 60 of 277
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)