Exam 9: Large-Sample Tests of Hypotheses
Exam 1: Describing Data With Graphs94 Questions
Exam 2: Describing Data With Numerical Measures186 Questions
Exam 3: Describing Bivariate Data35 Questions
Exam 4: Probability and Probability Distributions136 Questions
Exam 5: Several Useful Discrete Distributions129 Questions
Exam 6: The Normal Probability Distribution196 Questions
Exam 7: Sampling Distributions162 Questions
Exam 8: Large-Sample Estimation173 Questions
Exam 9: Large-Sample Tests of Hypotheses210 Questions
Exam 10: Inference From Small Samples261 Questions
Exam 11: The Analysis of Variance156 Questions
Exam 12: Linear Regression and Correlation165 Questions
Exam 13: Multiple Regression Analysis178 Questions
Exam 14: Analysis of Categorical Data136 Questions
Exam 15: Nonparametric Statistics198 Questions
Select questions type
Suppose in testing a hypothesis about a proportion, the z test statistic is computed to be 1.92. The null hypothesis should be rejected if the chosen level of significance is 0.01 and a two-tailed test is used.
(True/False)
4.9/5  (33)
(33)
When the necessary conditions are met, a two-tailed test is being conducted to test the difference between two population proportions. The two sample proportions are 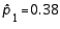 and
and 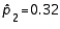 , respectively, and the standard error of the sampling distribution of
, respectively, and the standard error of the sampling distribution of 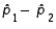 is 0.04. Then, the calculated value of the test statistic will be 1.50.
is 0.04. Then, the calculated value of the test statistic will be 1.50.
(True/False)
4.9/5  (40)
(40)
Which of the following statements about possible errors in hypothesis tests is correct?
(Multiple Choice)
4.8/5  (37)
(37)
If a hypothesis test leads to incorrectly rejecting the null hypothesis, a Type II error has been committed.
(True/False)
4.9/5  (37)
(37)
If the probability of committing a Type I error is set at 0.10, then the probability of committing a Type II error will be 0.90, since sum of probabilities must be 1.0.
(True/False)
4.8/5  (39)
(39)
A manufacturer of copper pipes must produce pipes with a diameter of precisely 5 inches. The firm's quality inspector wants to test the hypothesis that pipes of the proper size are being produced. Accordingly, a simple random sample of 100 pipes is taken from the production process. The sample mean diameter turns out to be 4.98 inches and the sample standard deviation 0.2 inches. Using a significance level of 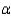 = 0.05, test the appropriate hypotheses.
Find the p-value for the test.
Test statistic = ______________
p-value = ______________
Conclusion: ______________
Interpretation: __________________________________________
= 0.05, test the appropriate hypotheses.
Find the p-value for the test.
Test statistic = ______________
p-value = ______________
Conclusion: ______________
Interpretation: __________________________________________
(Essay)
4.8/5  (29)
(29)
Suppose that we reject the null hypothesis 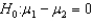 at the 0 .05 level of significance. Then for which of the following
at the 0 .05 level of significance. Then for which of the following 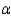 -values do we also reject the null hypothesis?
-values do we also reject the null hypothesis?
(Multiple Choice)
4.8/5  (28)
(28)
Increasing the size of the samples in a study to estimate the difference between two population means will increase the probability of committing a Type I error that a decision maker can have regarding the interval estimate.
(True/False)
4.8/5  (30)
(30)
If H0 is corroborated in a hypothesis test, no action need be taken by anyone.
(True/False)
4.9/5  (42)
(42)
The sampling distribution of 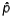 is approximately normal, provided that the sample size is large enough (n > 30).
is approximately normal, provided that the sample size is large enough (n > 30).
(True/False)
4.9/5  (33)
(33)
A statistics professor has claimed that her top student will average more than 98 points in the final exam. If you wish to test this claim, you would formulate the following null and alternative hypotheses: 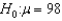 vs.
vs. 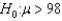 .
.
(True/False)
4.8/5  (32)
(32)
When the hypothesized proportion 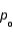 is close to 0.50, the spread in the sampling distribution of the sample proportion
is close to 0.50, the spread in the sampling distribution of the sample proportion 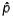 is greater than when
is greater than when 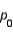 is close to 0.0 or 1.0.
is close to 0.0 or 1.0.
(True/False)
4.8/5  (30)
(30)
The p-value of a statistical test is the largest value of the significance level 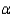 for which the null hypothesis can be rejected.
for which the null hypothesis can be rejected.
(True/False)
4.7/5  (40)
(40)
Type II error is typically greater for two-tailed hypothesis tests than for one-tailed tests.
(True/False)
4.8/5  (29)
(29)
In a one-tailed test, the p-value is found to be equal to 0.036. If the test had been two-tailed, the p-value would have been 0.072.
(True/False)
4.8/5  (34)
(34)
A two-tail test is a test in which a null hypothesis can be rejected by an extreme result occurring in only one direction.
(True/False)
4.9/5  (37)
(37)
A sample of size 150 is to be used to test the hypotheses H0: 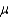 = 8.3 versus H1:
= 8.3 versus H1: 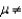 8.3 where
8.3 where 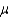 is the true average weight of a newborn American baby. Give the appropriate rejection region associated with each of the following significance levels.
is the true average weight of a newborn American baby. Give the appropriate rejection region associated with each of the following significance levels. 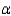 = 0.01
Critical Value(s) = ______________
= 0.01
Critical Value(s) = ______________ 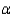 = 0.05
Critical Value(s) = ______________
= 0.05
Critical Value(s) = ______________ 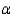 = 0.1
Critical Value(s) = ______________
= 0.1
Critical Value(s) = ______________
(Short Answer)
5.0/5  (30)
(30)
If you wish to estimate the difference between two population means using two independent large samples, the 90% confidence interval estimate can be constructed using which of the following critical values?
(Multiple Choice)
4.8/5  (28)
(28)
Showing 61 - 80 of 210
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)