Exam 9: Large-Sample Tests of Hypotheses
Exam 1: Describing Data With Graphs94 Questions
Exam 2: Describing Data With Numerical Measures186 Questions
Exam 3: Describing Bivariate Data35 Questions
Exam 4: Probability and Probability Distributions136 Questions
Exam 5: Several Useful Discrete Distributions129 Questions
Exam 6: The Normal Probability Distribution196 Questions
Exam 7: Sampling Distributions162 Questions
Exam 8: Large-Sample Estimation173 Questions
Exam 9: Large-Sample Tests of Hypotheses210 Questions
Exam 10: Inference From Small Samples261 Questions
Exam 11: The Analysis of Variance156 Questions
Exam 12: Linear Regression and Correlation165 Questions
Exam 13: Multiple Regression Analysis178 Questions
Exam 14: Analysis of Categorical Data136 Questions
Exam 15: Nonparametric Statistics198 Questions
Select questions type
Which of the following is an example of a null hypothesis?
(Multiple Choice)
4.7/5  (37)
(37)
For a fixed sample size n, as the probability of a Type II error 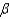 decreases, the probability of a Type I error
decreases, the probability of a Type I error 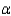 increases.
increases.
(True/False)
4.8/5  (44)
(44)
In testing 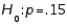 vs.
vs. 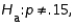 the level of significance must be twice as large as when testing
the level of significance must be twice as large as when testing 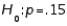 vs.
vs. 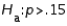 .
.
(True/False)
4.7/5  (35)
(35)
A Type I error for a statistical test is committed if we reject the null hypothesis when it is true.
(True/False)
4.9/5  (36)
(36)
If we reject the null hypothesis 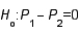 , we conclude that there is not enough statistical evidence to infer that the population proportions are equal.
, we conclude that there is not enough statistical evidence to infer that the population proportions are equal.
(True/False)
4.9/5  (28)
(28)
Consider testing the hypothesis:  . If the value of the test statistic is equal to 1.36, then the p-value is:
. If the value of the test statistic is equal to 1.36, then the p-value is:
(Multiple Choice)
4.8/5  (30)
(30)
In constructing a confidence interval estimate for the difference between two population proportions, we:
(Multiple Choice)
4.9/5  (43)
(43)
When the necessary conditions are met, a lower tailed test is being conducted for the difference between two population proportions. If the value of the test statistic is -2.50, then the p-value is 0.0062.
(True/False)
4.8/5  (34)
(34)
In testing 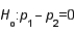 vs.
vs. 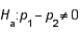 using a significance level equal to .05, the critical value that will be used to conduct the test is z = 1.645.
using a significance level equal to .05, the critical value that will be used to conduct the test is z = 1.645.
(True/False)
4.8/5  (31)
(31)
A two-tailed test of hypothesis for a population mean 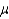 with a significance level
with a significance level 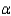 equal to .05 will have a critical value z equal to .475.
equal to .05 will have a critical value z equal to .475.
(True/False)
4.8/5  (30)
(30)
A hypothesis that specifies a range of values for the unknown parameter is called an interval estimate.
(True/False)
4.8/5  (28)
(28)
In a two-tail test for the population proportion, if the null hypothesis is rejected when the alternative hypothesis is false, a Type I error is committed.
(True/False)
4.9/5  (43)
(43)
In selecting the sample size to estimate the population proportion p, if we have no knowledge of even the approximate values of the sample proportion 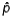 , we:
, we:
(Multiple Choice)
4.9/5  (35)
(35)
The null hypothesis is a vehicle for making startling new claims that contradict the conventional wisdom, that assert "guilt without a reasonable doubt."
(True/False)
4.9/5  (32)
(32)
A sample of size 150 from population 1 has 40 successes. A sample of size 250 from population 2 has 30 successes. The value of the test statistic for testing the null hypothesis that the proportion of successes in population one exceeds the proportion of successes in population two by 0.05 is:
(Multiple Choice)
4.9/5  (42)
(42)
Which of the following exemplifies a Type I error of incorrectly rejecting a true null hypothesis?
(Multiple Choice)
4.8/5  (38)
(38)
In estimating the difference between two population means, the following summary statistics were found: 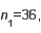
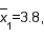
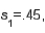
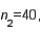
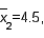 and
and 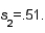 Based on these results, the point estimate of
Based on these results, the point estimate of 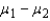 is .70.
is .70.
(True/False)
4.9/5  (37)
(37)
In testing the hypotheses
H0: p1 - p2 = 0.10 vs.
Ha: 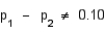 .
Use the following statistics, where x1 and x2 represent the number of Dial Soap sales in the two samples, respectively.
n1 = 150, x1 = 72
n2 = 175, x2 = 70
What conclusion can we draw at the 5% significance level?
Test statistic = ______________
Critical Value(s) = ______________
Conclusion: ______________
What is the p-value of the test?
p-value = ______________
Explain how to use the p-value to test the hypotheses.
____________________________
Estimate with 95% confidence the difference between the two population proportions.
______________
Interpret and explain how to use the confidence interval to test the hypotheses.
__________________________________________
.
Use the following statistics, where x1 and x2 represent the number of Dial Soap sales in the two samples, respectively.
n1 = 150, x1 = 72
n2 = 175, x2 = 70
What conclusion can we draw at the 5% significance level?
Test statistic = ______________
Critical Value(s) = ______________
Conclusion: ______________
What is the p-value of the test?
p-value = ______________
Explain how to use the p-value to test the hypotheses.
____________________________
Estimate with 95% confidence the difference between the two population proportions.
______________
Interpret and explain how to use the confidence interval to test the hypotheses.
__________________________________________
(Essay)
4.9/5  (38)
(38)
After calculating the sample size needed to estimate a population proportion to within 0.04, your statistics professor told you the maximum allowable error must be reduced to just .01. If the original calculation led to a sample size of 800, the sample size will now have to be:
(Multiple Choice)
4.7/5  (34)
(34)
Showing 141 - 160 of 210
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)