Exam 9: Large-Sample Tests of Hypotheses
Exam 1: Describing Data With Graphs94 Questions
Exam 2: Describing Data With Numerical Measures186 Questions
Exam 3: Describing Bivariate Data35 Questions
Exam 4: Probability and Probability Distributions136 Questions
Exam 5: Several Useful Discrete Distributions129 Questions
Exam 6: The Normal Probability Distribution196 Questions
Exam 7: Sampling Distributions162 Questions
Exam 8: Large-Sample Estimation173 Questions
Exam 9: Large-Sample Tests of Hypotheses210 Questions
Exam 10: Inference From Small Samples261 Questions
Exam 11: The Analysis of Variance156 Questions
Exam 12: Linear Regression and Correlation165 Questions
Exam 13: Multiple Regression Analysis178 Questions
Exam 14: Analysis of Categorical Data136 Questions
Exam 15: Nonparametric Statistics198 Questions
Select questions type
Reducing the probability of a Type I error also reduces the probability of a Type II error.
(True/False)
4.9/5  (38)
(38)
A survey claims that 9 out of 10 doctors recommend aspirin for their patients with headaches. To test this claim against the alternative that the actual proportion of doctors who recommend aspirin is less than 0.90, a random sample of 100 doctors' results in 83 who indicate that they recommend aspirin. The value of the test statistic in this problem is approximately equal to:
(Multiple Choice)
4.8/5  (32)
(32)
A new light bulb is being considered for use in an office with computers. It is decided that the new bulb will only be used if it has a mean lifetime of more than 500 hours. A random sample of 40 bulbs is selected and placed on life test. The mean and standard deviation are found to be 505 hours and 18 hours, respectively. Perform the appropriate test of hypothesis to determine whether the new bulb should be used. Use a 0.01 level of significance.
Test statistic = ______________
Critical Value(s) = ______________
Conclusion: ______________
Interpretation: __________________________________________
(Essay)
4.8/5  (36)
(36)
An experiment was conducted to test the effect of a new drug on a viral infection. The infection was induced in 100 mice, and the mice were randomly split into two groups of 50. The first group, the control group, received no treatment for the infection. The second group received the drug. The proportions of survivors, 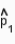 and
and 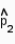 , in the two groups after a 30-day period, were found to be 0.40 and 0.64, respectively. Is there sufficient evidence to indicate that the drug is effective in treating the viral infection? Use
, in the two groups after a 30-day period, were found to be 0.40 and 0.64, respectively. Is there sufficient evidence to indicate that the drug is effective in treating the viral infection? Use 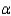 = 0.05.
Test statistic = ______________
Critical Value(s) = ______________
Conclusion: ______________
Interpretation: __________________________________________
Use a 95% confidence interval to estimate the actual difference in the cure rates for the treated versus the control groups.
______________
= 0.05.
Test statistic = ______________
Critical Value(s) = ______________
Conclusion: ______________
Interpretation: __________________________________________
Use a 95% confidence interval to estimate the actual difference in the cure rates for the treated versus the control groups.
______________
(Short Answer)
4.9/5  (28)
(28)
A one-tailed hypothesis test of the population proportion is used when the alternative hypothesis takes the form 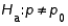 .
.
(True/False)
4.8/5  (35)
(35)
Which of the following correctly describes hypothesis testing?
(Multiple Choice)
4.8/5  (37)
(37)
In testing 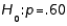 vs.
vs. 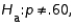 the test statistic value is found to be equal to 1.20. The p-value for this test would be approximately .1151.
the test statistic value is found to be equal to 1.20. The p-value for this test would be approximately .1151.
(True/False)
4.9/5  (32)
(32)
Two independent samples of sizes 40 and 50 are randomly selected from two populations to test the difference between the population means 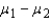 . The sampling distribution of the sample mean difference
. The sampling distribution of the sample mean difference 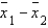 is:
is:
(Multiple Choice)
4.7/5  (30)
(30)
In a one-tail test about the population proportion p, the p-value is found to be equal to 0.0352. If the test had been two-tail, the p-value would have been 0.0704.
(True/False)
4.7/5  (28)
(28)
As the significance level 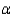 increases, the probability of a Type I error increases and the size of the rejection region increases.
increases, the probability of a Type I error increases and the size of the rejection region increases.
(True/False)
5.0/5  (32)
(32)
A student government representative at a local university claims that 60% of the undergraduate students favor a move to Division I in college football. A random sample of 250 undergraduate students was selected and 140 students indicated they favored a move to Division I.
Perform the appropriate test of hypothesis to test the representative's claim. Use 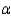 = 0.05.
Test statistic = ______________
Critical Value(s) = ______________
Conclusion: ______________
Interpretation: __________________________________________
Find the p-value for this test.
p-value = ______________
= 0.05.
Test statistic = ______________
Critical Value(s) = ______________
Conclusion: ______________
Interpretation: __________________________________________
Find the p-value for this test.
p-value = ______________
(Essay)
4.7/5  (37)
(37)
A two-tailed hypothesis test of the population proportion takes the form 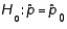 vs.
vs. 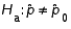 .
.
(True/False)
4.9/5  (34)
(34)
Independent random samples of n1 = 150 and n2 = 150 sales phone calls for an insurance policy were randomly selected from binomial populations 1 and 2, respectively. Sample 1 had 80 successful sales, and sample 2 had 88 successful sales. Suppose you have no preconceived theory concerning which parameter, p1 or p2, is the larger and you wish to detect only a difference between the two parameters if one exists.
Calculate the standard error of the difference in the two sample proportions, 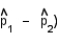 . Make sure to use the pooled estimate for the common value of p.
______________
Calculate the test statistic that you would use for the test above. Based on your knowledge of the standard normal distribution, is this a likely or unlikely observation, assuming that H0 is true and the two population proportions are the same?
Test statistic = ______________
Find the p-value for the test. Test for a significant difference in the population means at the 1% significance level.
p-value = ______________
Find the rejection region when
. Make sure to use the pooled estimate for the common value of p.
______________
Calculate the test statistic that you would use for the test above. Based on your knowledge of the standard normal distribution, is this a likely or unlikely observation, assuming that H0 is true and the two population proportions are the same?
Test statistic = ______________
Find the p-value for the test. Test for a significant difference in the population means at the 1% significance level.
p-value = ______________
Find the rejection region when 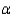 = 0.01. Do the data provide sufficient evidence to indicate a difference in the population proportions?
Critical Value(s) = ______________
Conclusion: ______________
Interpretation: __________________________________________
= 0.01. Do the data provide sufficient evidence to indicate a difference in the population proportions?
Critical Value(s) = ______________
Conclusion: ______________
Interpretation: __________________________________________
(Short Answer)
4.8/5  (39)
(39)
In order to calculate the p-value associated with a test, it is necessary to know the level of significance 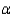 .
.
(True/False)
4.7/5  (26)
(26)
If you wish to conduct a hypothesis test using a small significance level 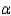 , you should have a large sample size to avoid committing a Type II error.
, you should have a large sample size to avoid committing a Type II error.
(True/False)
4.7/5  (33)
(33)
If the hypothesis test is conducted using 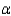 = .025, this means that:
= .025, this means that:
(Multiple Choice)
4.7/5  (33)
(33)
Showing 81 - 100 of 210
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)