Exam 10: Inference From Small Samples

A Marine drill instructor recorded the time in which each of 15 recruits completed an obstacle course both before and after basic training. To test whether any improvement occurred, the instructor would use a t-distribution with 15 degrees of freedom.

The equal-variances test statistic of 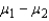is Student t distributed with 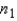+ 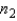degrees of freedom, provided that the two populations are normal.

In constructing 95% confidence interval estimate for the difference between the means of two normally distributed populations, where the unknown population variances are assumed not to be equal, summary statistics computed from two independent samples are as follows: 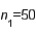, , 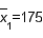, , 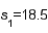, 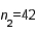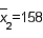and 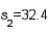. The upper confidence limit is:

Which of the following statements is true when small samples are used to estimate the true population mean where the population standard deviation is unknown?

The test for the equality of two population variances assumes that each of the two populations is normally distributed.

In making inferences about a population mean 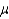, the degrees of freedom used in t-distribution are equal to the sample size.

The quantity 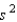is called the pooled variance estimate of the common variance of two unknown but equal population variances. It is the weighted average of the two sample variances, where the weights represent the:

Both the equal-variances and unequal variances test statistic and confidence interval estimator of 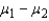require that the two populations be normally distributed.

The sampling distribution used to make inferences about a single population variance is:

The t distribution table in your test shows:

The shape of the chi-squared distribution depends on:

When the population variances are unequal, we estimate each population variance with its sample variance. Hence, the unequal-variances test statistic of 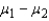is Student t distributed with 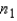+ 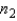-2 degrees of freedom.

Two independent samples of sizes 40 and 50 are randomly selected from two populations to test the difference between the population means 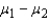. The sampling distribution of the sample mean difference 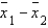is:

Researchers determine that 60 Kleenex tissues is the average number of tissues used during a cold. Suppose a random sample of 100 Kleenex users yielded the following statistics on the number of tissues used during a cold: 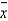= 52 and s = 22. Using the sample information provided, the value of the test statistic is:

The following data were drawn from a normal population: 15, 4, 24, 8, 16, 13, 9, 15, 7, and 22. Estimate the population mean with 90% confidence. LCL: ______________ UCL: ______________

A garment manufacturing company recorded the amount of time that it took to make a pair of jeans on 8 different occasions. The times in minutes are as follows: 12.5, 13.0, 11.9, 10.2, 13.1, 13.6, 13.8, and 14.0. Assume these measurements were taken from a population with a normal distribution. It is of interest to know if the sample data suggest that the average time it takes this company to make a pair of jeans is less than 13.5 minutes. Does the sample data support the alternative hypothesis at the 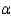= 0.05 level? Test statistic = ______________ Critical Value(s) = ______________ Conclusion: ______________ Interpretation: The average time it takes this company to make a pair of jeans ______________ less than 13.5 minutes. Construct a 95% confidence interval for the mean amount of time it takes this company to make a pair of jeans. ______________

In testing the hypothese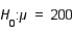s vs. 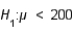, the sample mean is found to be 120. The null hypothesis:

Based on sample data, the 90% confidence interval limits for the population mean are LCL = 170.86 and UCL = 195.42. If the 10% level of significance were used in testing the hypothese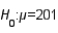s vs. 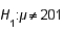, the null hypothesis:

If a sample has 15 observations and a 90% confidence estimate for 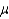is needed, the appropriate t-score is 1.341.

In testing the difference between two population means using two independent samples, we use the pooled variance in estimating the standard error of the sampling distribution of the sample mean difference 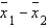if: