Exam 12: Multiple Integrals
Exam 1: Functions and Models118 Questions
Exam 2: Limits and Derivatives127 Questions
Exam 3: Differentiation Rules248 Questions
Exam 4: Applications of Differentiation273 Questions
Exam 5: Integrals239 Questions
Exam 6: Applications of Integration189 Questions
Exam 7: Differential Equations154 Questions
Exam 8: Infinite Sequences and Series341 Questions
Exam 9: Vectors and the Geometry of Space269 Questions
Exam 10: Vector Functions111 Questions
Exam 11: Partial Derivatives294 Questions
Exam 12: Multiple Integrals270 Questions
Exam 13: Vector Calculus240 Questions
Select questions type
Evaluate the triple integral in spherical coordinates, where E is the solid in the first octant bounded by the sphere and the coordinate planes.
(Multiple Choice)
4.9/5  (33)
(33)
Rewrite as an iterated integral with x as the variable of integration in the outer integral, where R is the region shown below. 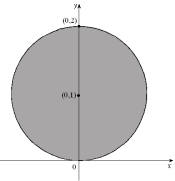
(Essay)
4.9/5  (36)
(36)
Rewrite the integral in terms of polar coordinates, then evaluate the integral.
(Essay)
4.8/5  (34)
(34)
Evaluate the triple integral in cylindrical coordinates, where .
(Multiple Choice)
4.7/5  (36)
(36)
Use the change of variables x = 2u + 3v, y = 3u - 2v to evaluate , where R is the square with vertices (0, 0), (2, 3), (5, 1), and (3, -2).
(Short Answer)
4.9/5  (30)
(30)
Find the volume of the solid bounded by the paraboloid and the plane .
(Multiple Choice)
4.9/5  (32)
(32)
Compute the Jacobian of the transformation T given by , , and find the image of under T.
(Essay)
4.9/5  (34)
(34)
A greenhouse is shown below. It is 10 ft wide and 20 ft long and has a at roof that is 12 ft high at one corner and 10 ft high at each of the adjacent corners. Find the volume of the greenhouse. 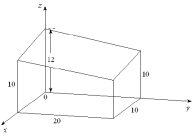
(Short Answer)
4.9/5  (21)
(21)
(a) Sketch the solid whose volume is given by the iterated integral .(b) Rewrite the integral in part (a) as an equivalent iterated integral (or integrals) in the order dx, dz, dy.(c) Rewrite the integral in part (a) as an equivalent iterated integral (or integrals) in the order dy, dz, dx.
(Essay)
5.0/5  (37)
(37)
Let E be the solid under and above the region in the xy-plane bounded by x + y = 1 and x + y = 2. Sketch the solid, then express the volume of E as an iterated integral in rectangular coordinates.
(Essay)
4.9/5  (41)
(41)
Find , where S is the solid bounded by the cylinder and the planes z = 0, y = 1, and z = y.
(Short Answer)
4.8/5  (33)
(33)
Find the area of the part of the plane x +y + z = 6 that lies above the square with vertices (0, 0), (1, 0), (0, 1), and (1, 1).
(Multiple Choice)
4.9/5  (34)
(34)
Change the order of integration in the following integral and evaluate: .
(Essay)
4.7/5  (28)
(28)
Give an example of a non-constant function f(x, y) such that the average value of f over is 0.
(Essay)
4.8/5  (24)
(24)
Calculate the double Riemann sum of f for the partition of R given by the indicated lines and the given choice of . , , , , , , , ; = lower left corner of Rij.
(Short Answer)
4.8/5  (37)
(37)
Let E be the solid under the paraboloid , above the xy-plane, and between the planes x = 2 and x = 3. Express the volume of E as an iterated integral in rectangular coordinates.
(Short Answer)
4.8/5  (35)
(35)
Showing 221 - 240 of 270
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)