Exam 12: Multiple Integrals
Exam 1: Functions and Models118 Questions
Exam 2: Limits and Derivatives127 Questions
Exam 3: Differentiation Rules248 Questions
Exam 4: Applications of Differentiation273 Questions
Exam 5: Integrals239 Questions
Exam 6: Applications of Integration189 Questions
Exam 7: Differential Equations154 Questions
Exam 8: Infinite Sequences and Series341 Questions
Exam 9: Vectors and the Geometry of Space269 Questions
Exam 10: Vector Functions111 Questions
Exam 11: Partial Derivatives294 Questions
Exam 12: Multiple Integrals270 Questions
Exam 13: Vector Calculus240 Questions
Select questions type
Let , and let . Let R be its own partition, and let be the center of R. Calculate the double Riemann sum of f.
(Multiple Choice)
4.9/5  (36)
(36)
Find the volume of the region above the paraboloid and below the hemisphere .
(Short Answer)
4.9/5  (34)
(34)
Use the Midpoint Rule to estimate over partitioned by the lines x = 1 and y = 1. Then estimate the average value of over R.
(Essay)
4.9/5  (29)
(29)
Suppose X and Y are random variables. Find k such that the function is a joint density function.
(Multiple Choice)
4.7/5  (29)
(29)
Let T be the transformation given by x = 2u + v, y = u + 2v.(a) A region S in the uv-plane is given below. Sketch the image R of S in the xy-plane. 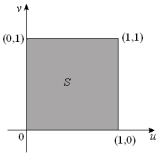 (b) Find the inverse transformation .(c) Evaluate the double integral .
(b) Find the inverse transformation .(c) Evaluate the double integral .
(Essay)
4.7/5  (30)
(30)
Compute the Riemann sum for the double integral where for the given grid and choice of sample points. ![Compute the Riemann sum for the double integral \iint _ { R } x + 2 y d A where R = [ 0,6 ] \times [ 0,2 ] for the given grid and choice of sample points.](https://storage.examlex.com/TB2033/11eaa8e2_1039_571b_96ab_7183d782fe0a_TB2033_00.jpg)
(Short Answer)
4.9/5  (36)
(36)
Evaluate where by first identifying it as the volume of a solid.
(Short Answer)
4.7/5  (39)
(39)
Rewrite as an iterated integral with y as the variable of integration in the outer integral, where R is the region shown below. 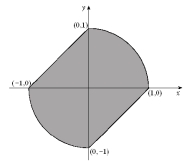
(Essay)
4.8/5  (37)
(37)
Evaluate the integral , where R is the region enclosed by the ellipse .
(Multiple Choice)
4.7/5  (28)
(28)
Let E be the solid that lies below the sphere and above the cone , where . Find the value of the triple integral .
(Multiple Choice)
4.9/5  (27)
(27)
Find the surface area of the part of the cone lying inside the cylinder .
(Short Answer)
4.9/5  (31)
(31)
Compute the Jacobian of the transformation T given by , . Compute the area of the image of and compare it to the area of S.
(Essay)
4.8/5  (36)
(36)
Describe the region sketched below both as a type I and as a type II region. 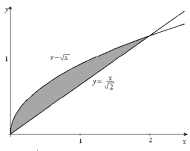
(Essay)
4.7/5  (33)
(33)
Find the surface area for the part of the plane that lies inside the elliptic cylinder .
(Short Answer)
4.9/5  (34)
(34)
Showing 81 - 100 of 270
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)