Exam 12: Multiple Integrals
Exam 1: Functions and Models118 Questions
Exam 2: Limits and Derivatives127 Questions
Exam 3: Differentiation Rules248 Questions
Exam 4: Applications of Differentiation273 Questions
Exam 5: Integrals239 Questions
Exam 6: Applications of Integration189 Questions
Exam 7: Differential Equations154 Questions
Exam 8: Infinite Sequences and Series341 Questions
Exam 9: Vectors and the Geometry of Space269 Questions
Exam 10: Vector Functions111 Questions
Exam 11: Partial Derivatives294 Questions
Exam 12: Multiple Integrals270 Questions
Exam 13: Vector Calculus240 Questions
Select questions type
A solid is bounded above by the paraboloid and below by the xy-plane. Compute the volume of this solid using polar coordinates.
(Essay)
4.8/5  (35)
(35)
Use a double integral to find the area of the region enclosed by one loop of the curve .
(Multiple Choice)
4.8/5  (32)
(32)
The average value of f(x, y) over a region D in the plane with area A(D) is . Find the average value of f(x, y) = xy over the region .
(Short Answer)
4.8/5  (34)
(34)
Calculate the double Riemann sum of f for the partition of R given by the indicated lines and the given choice of . , , x = 1, y = 1, y = 2; = center of Rij.
(Short Answer)
4.9/5  (41)
(41)
Evaluate , where E is the solid bounded by the cylinder , above by z = 3 and below by z = 0.
(Short Answer)
4.9/5  (34)
(34)
Write as an iterated integral in polar coordinates, where R is the region shown below. 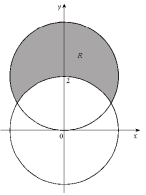
(Essay)
4.7/5  (38)
(38)
A region W in is described completely by , , , and .(a) Describe or sketch this region. 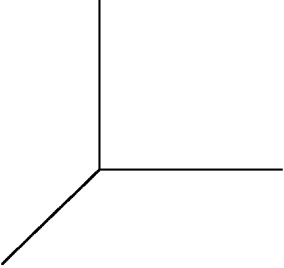 (b) Write an integral in rectangular coordinates which gives the volume of W. Do not work out this integral.(c) Write an integral in spherical coordinates which gives the volume of W. Find the volume of W using this integral.
(b) Write an integral in rectangular coordinates which gives the volume of W. Do not work out this integral.(c) Write an integral in spherical coordinates which gives the volume of W. Find the volume of W using this integral.
(Essay)
4.9/5  (29)
(29)
Compute the Riemann sum for the double integral where for the given grid and choice of sample points. ![Compute the Riemann sum for the double integral \iint _ { R } x + 2 y d A where R = [ 0,6 ] \times [ 0,2 ] for the given grid and choice of sample points.](https://storage.examlex.com/TB2033/11eaa8e2_1039_f35e_96ab_4df2e1c95f95_TB2033_00.jpg)
(Short Answer)
4.9/5  (42)
(42)
Let T be the transformation given by x = 2u + v, y = 3u.(a) A region S in the uv-plane is given below. Sketch the image R of S in the xy-plane. 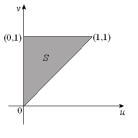 (b) Find the inverse transformation .(c) Evaluate the double integral .
(b) Find the inverse transformation .(c) Evaluate the double integral .
(Essay)
4.9/5  (30)
(30)
Find the volume under the paraboloid above the triangle with vertices (0, 0, 0), (3, 0, 0), and (3, 1, 0).
(Multiple Choice)
4.8/5  (32)
(32)
Find the area of that part of the plane that lies above the rectangle [1, 4] [2, 4].
(Short Answer)
4.8/5  (45)
(45)
A phonograph turntable is made in the shape of a circular disk of radius 6 inches with density function . Find the mass of the disk.
(Multiple Choice)
4.8/5  (35)
(35)
Write as an iterated integral in polar coordinates, where R is the region shown below. 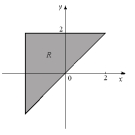
(Essay)
4.8/5  (38)
(38)
Showing 181 - 200 of 270
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)