Exam 12: Multiple Integrals
Exam 1: Functions and Models118 Questions
Exam 2: Limits and Derivatives127 Questions
Exam 3: Differentiation Rules248 Questions
Exam 4: Applications of Differentiation273 Questions
Exam 5: Integrals239 Questions
Exam 6: Applications of Integration189 Questions
Exam 7: Differential Equations154 Questions
Exam 8: Infinite Sequences and Series341 Questions
Exam 9: Vectors and the Geometry of Space269 Questions
Exam 10: Vector Functions111 Questions
Exam 11: Partial Derivatives294 Questions
Exam 12: Multiple Integrals270 Questions
Exam 13: Vector Calculus240 Questions
Select questions type
Find the moment of inertia about the x-axis and the moment of inertia about the y-axis for the region in the first quadrant bounded by y = x and , assuming p = 1.
(Essay)
4.9/5  (34)
(34)
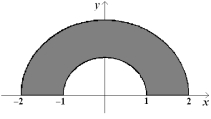
Find the y-coordinate of the centroid of the semiannular plane region given by , . Sketch the plane region and plot the centroid in the graph.
(Essay)
4.8/5  (39)
(39)
Use cylindrical coordinates to find , where R is the region bounded by and .
(Essay)
4.9/5  (31)
(31)
Find the volume of the solid in the first octant that is bounded by the plane y + z = 4, the cylinder , and the xy- and yz-planes.
(Short Answer)
4.8/5  (31)
(31)
Find a transformation x = x (u, v), y = y (u, v) maps the region in the uv-plane into the xy-plane. 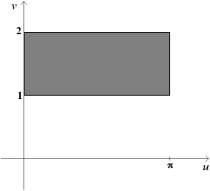
(Short Answer)
4.8/5  (33)
(33)
Give a geometric description of the solid S whose volume in spherical coordinates is given by .
(Essay)
4.7/5  (29)
(29)
Evaluate the triple integral , where E is the solid bounded by the coordinate planes and the plane 2x + y + z = 4.
(Multiple Choice)
4.8/5  (38)
(38)
Evaluate by making an appropriate change of variables, where R is the region in the first quadrant bounded by the ellipse .
(Essay)
4.9/5  (31)
(31)
Rewrite as an iterated integral with y as the variable of integration in the
outer integral, where R is the region shown below. 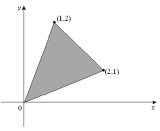
(Essay)
4.9/5  (29)
(29)
Rewrite the integral in terms of polar coordinates, then evaluate the integral.
(Essay)
4.9/5  (28)
(28)
Evaluate the triple integral in spherical coordinates, where E is the solid bounded by the hemisphere and the plane z = 0.
(Multiple Choice)
4.9/5  (45)
(45)
Evaluate , where E is the solid bounded by the sphere and the cone .
(Short Answer)
4.7/5  (27)
(27)
Evaluate the iterated integral by converting to polar coordinates.
(Multiple Choice)
4.8/5  (38)
(38)
Find the y-coordinate of the center of mass of the lamina that occupies the region and whose density function at any point is the distance from that point to the y-axis.
(Multiple Choice)
4.9/5  (37)
(37)
Write as an iterated integral in polar coordinates, where R is the region shown below. 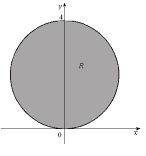
(Essay)
4.8/5  (27)
(27)
Find a transformation x = x (u, v), y = y (u, v) maps the region in the uv-plane into the xy-plane. 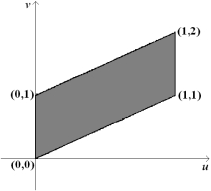
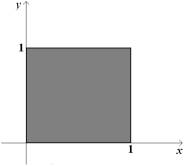
(Short Answer)
4.9/5  (26)
(26)
Showing 101 - 120 of 270
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)