Exam 8: Regression, Associations, and Predictive Modeling
Exam 1: Exploring and Understanding Data125 Questions
Exam 2: Exploring Relationships Between Variables165 Questions
Exam 3: Gathering Data111 Questions
Exam 4: Randomness and Probability148 Questions
Exam 5: From the Data at Hand to the World at Large128 Questions
Exam 6: Accessing Associations Between Variables93 Questions
Exam 7: Inference When Variables Are Related25 Questions
Exam 8: Regression, Associations, and Predictive Modeling792 Questions
Select questions type
Time Wasted A group of students decide to see if there is link between wasting time on the
internet and GPA. They don't expect to find an extremely strong association, but they're
hoping for at least a weak relationship. Here are the findings. linear regression results: Dependent Variable: GPA Sample size: 10 R (correlation coefficient) =-0.37199274 R-sq =0.1383786 s=0.85365134 Parameter Estimate Std. Err. Intercept 4.06191 0.74405 Hours/week -0.0297 0.02616
a. How strong is the relationship the students found? Describe in context with statistical
justification.
One student is concerned that the relationship is so weak, there may not actually be any
relationship at all. To test this concern, he runs a simulation where the 10 GPA's are
randomly matched with the 10 hours/week. After each random assignment, the correlation
is calculated. This process is repeated 100 times. Here is a histogram of the 100 correlations.
The correlation coefficient of -0.371 is indicated with a vertical line. 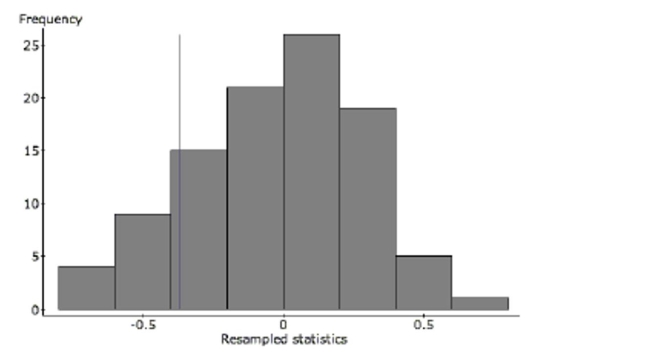 b. Do the results of this simulation confirm the suspicion that there may not be any
relationship? Refer specifically to the graph in your explanation.
b. Do the results of this simulation confirm the suspicion that there may not be any
relationship? Refer specifically to the graph in your explanation.
(Essay)
4.8/5  (41)
(41)
Too much TV? A father is concerned that his teenage son is watching too much television
each day, since his son watches an average of 2 hours per day. His son says that his TV
habits are no different than those of his friends. Since this father has taken a stats class, he
knows that he can actually test to see whether or not his son is watching more TV than his
peers. The father collects a random sample of television watching times from boys at his
son's high school and gets the following data:
1.9 2.3 2.2 1.9 1.6 2.6 1.4 2.0 2.0 2.2
Is the father right? That is, is there evidence that other boys average less than 2 hours of
television per day? Conduct a hypothesis test, making sure to state your conclusions in the
context of the problem.
(Essay)
4.8/5  (41)
(41)
Suppose that a manufacturer is testing one of its machines to make sure that the machine is producing more than good parts and . The test results in a -value of . Unknown to the manufacturer, the machine is actually producing good parts. What probably happens as a result of the testing?
(Multiple Choice)
4.9/5  (36)
(36)
Internet access A recent Gallup poll found that 28% of U.S. teens aged 13-17 have a
computer with Internet access in their rooms. The poll was based on a random sample of
1028 teens and reported a margin of error of
3%. What level of confidence did Gallup use
for this poll?
(Essay)
4.7/5  (38)
(38)
Listed below are the names of the 20 pharmacists on the hospital staff. Use the random
numbers listed below to select three of them to be in the sample. Clearly explain your
method. Pastore Back Spiridinov Ahl Hedge MacDowell Schissel Novelli Lavine Kaplan Highland Roundy Grubb Markowitz Glass Davies Golkowski Reeves Janis Yen
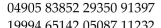
(Essay)
4.8/5  (45)
(45)
Which is true about randomized experiments?
I. Randomization reduces the effects of confounding variables.
II. Random assignment of treatments allows results to be generalized to the larger population.
III. Blocking can be used to reduce the within-treatment variability.
(Multiple Choice)
4.8/5  (35)
(35)
You could win a $1000 prize by tossing a coin in one of two games. To win Game A, you must get
Exactly 50% heads. To win Game B, you must get between 45% and 55% heads. Although which
Game you must play will be chosen randomly, then you may decide whether to toss the coin 20
Times or 50 times. How many tosses would you choose to make?
(Multiple Choice)
4.9/5  (35)
(35)
A researcher investigating whether joggers are less likely to get colds than people who do not jog
Found a P-value of 3%. This means that:
(Multiple Choice)
4.9/5  (41)
(41)
The United States Census collects data on many variables about individuals and households.
Which variable is categorical?
(Multiple Choice)
4.8/5  (44)
(44)
Preservative Leather furniture used in public places can fade, crack, and deteriorate
rapidly. An airport manager wants to see if a leather preservative spray can make the
furniture look good longer. He buys eight new leather chairs and places them in the
waiting area, four near the south-facing windows and the other four set back from the
windows as shown. He assigned the chairs randomly to these spots. 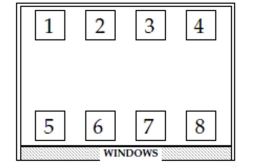 a. Use the random numbers given to decide which chairs to spray. Explain your method
clearly.
a. Use the random numbers given to decide which chairs to spray. Explain your method
clearly. 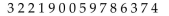 b. Briefly explain why your assignment strategy is important in helping the manager assess
the effectiveness of the leather preservative.
b. Briefly explain why your assignment strategy is important in helping the manager assess
the effectiveness of the leather preservative.
(Essay)
4.9/5  (31)
(31)
Blood pressure and cholesterol Suppose that both blood pressure and cholesterol levels of
adult women can be described with Normal models, and that the correlation between these
variables is 0.60. If a woman's blood pressure places her at the 88th percentile, at what
percentile would you predict her cholesterol level to be?
(Essay)
4.7/5  (49)
(49)
Show three trials by clearly labeling the random number table given below. Specify the
outcome for each trial. 
(Essay)
4.8/5  (34)
(34)
The next day, a young girl reveals that her older brother also went trick-or-treating, but
didn't want to admit that he participated. He was added to the data set and these are the
results. Dependent Variable: candy
Sample size: 10
(correlation coefficient
Parameter Estimate Std. Err. Intercept 13.569231 9.0783516 Age 3.4038462 1.0175376
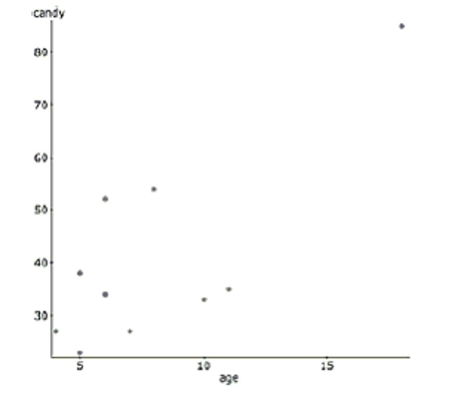 Describe the effect of this new candy collector on the regression model.
Describe the effect of this new candy collector on the regression model.
(Essay)
4.7/5  (32)
(32)
A statistics professor wants to see if more than 80% of her students enjoyed taking her class. At the End of the term, she takes a random sample of students from her large class and asks, in an Anonymous survey, if the students enjoyed taking her class. Which set of hypotheses should she
Test?
(Multiple Choice)
4.8/5  (35)
(35)
Doctors at a technology research facility randomly assigned equal numbers of people to use computer keyboards in two rooms. In one room a group of people typed a manuscript using standard keyboards, while in the other room people typed the same manuscript using ergonomic keyboards to see if those people could type more words per minute. After collecting data for several days the researchers tested the hypothesis against the one-tail alternative and found . Which is true?
(Multiple Choice)
4.9/5  (41)
(41)
If we wish to compare the average PSAT scores of boys and girls taking AP* Statistics at a high
School, which would be the best way to gather these data?
(Multiple Choice)
4.9/5  (40)
(40)
Identify the following:
a. the subjects
b. the factor(s) and the number of level(s) for each
c. the number of treatments
d. whether or not the experiment is blind (or double-blind)
e. the response variable
(Essay)
4.8/5  (35)
(35)
Showing 181 - 200 of 792
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)