Exam 8: Regression, Associations, and Predictive Modeling
Exam 1: Exploring and Understanding Data125 Questions
Exam 2: Exploring Relationships Between Variables165 Questions
Exam 3: Gathering Data111 Questions
Exam 4: Randomness and Probability148 Questions
Exam 5: From the Data at Hand to the World at Large128 Questions
Exam 6: Accessing Associations Between Variables93 Questions
Exam 7: Inference When Variables Are Related25 Questions
Exam 8: Regression, Associations, and Predictive Modeling792 Questions
Select questions type
Three brands of AAA batteries are compared to see which last longest. Each brand of
battery is tested in four different devices (a TV remote control, a hand-held game, a
miniature flashlight, and a digital camera). The experiment is run once for each
combination of brand and device. The twelve runs are ordered randomly. The time that the
each battery lasts (in minutes) under continuous usage is recorded. Device Brand A Brand B Brand C Remote 1320 1220 1250 Game 480 460 450 Light 245 225 240 Camera 81 72 77
The two-way ANOVA table for response variable Time and factors Brand and Device is
given below. 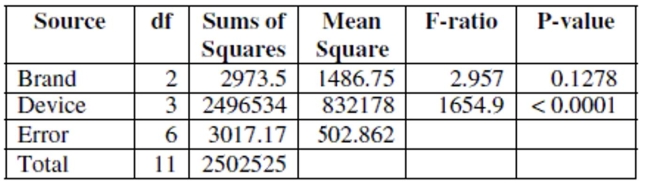 a. Write the model equation for this ANOVA. (Use symbols or words, no numbers.)
b. Test to see whether there is a brand effect. Write the hypotheses being tested, and state
your conclusion using a 5% level of significance. Write your conclusion in the context of
this problem.
c. Explain the role that the device factor plays in this analysis.
d. Can an interaction term be added to this model? Explain.
e. Use the plots below to check the ANOVA conditions.
a. Write the model equation for this ANOVA. (Use symbols or words, no numbers.)
b. Test to see whether there is a brand effect. Write the hypotheses being tested, and state
your conclusion using a 5% level of significance. Write your conclusion in the context of
this problem.
c. Explain the role that the device factor plays in this analysis.
d. Can an interaction term be added to this model? Explain.
e. Use the plots below to check the ANOVA conditions. 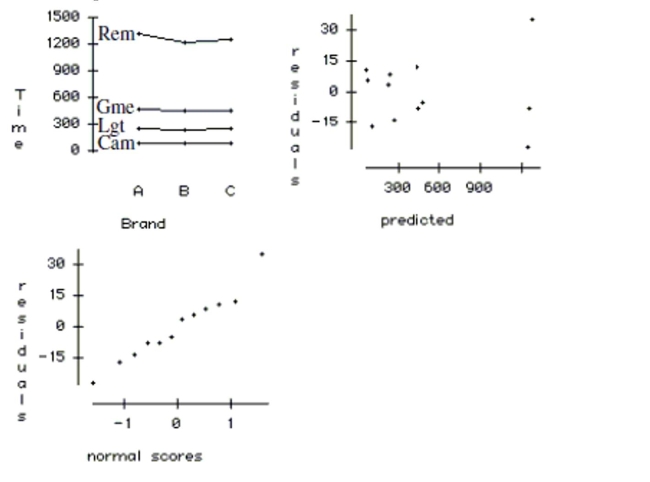
(Essay)
4.8/5  (33)
(33)
The veterinary bills for the dogs are summarized in the ogive shown. Estimate the IQR of these
Expenses. 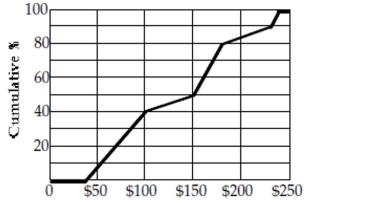
(Multiple Choice)
4.8/5  (34)
(34)
In an experiment the primary purpose of blocking is to reduce
(Multiple Choice)
4.9/5  (35)
(35)
We can tell that these two features are independent because…
A) The probability of having a kickstand given that you have a water bottle (56.7%) is about
equal to the probability of having a kickstand (55%).
B) These two features don't have anything to do with each other, so we know they're
independent.
C) The probability of having both features (34%) does not equal the probability of having neither
feature (19%).
D) The probability of having both features is not zero; it is 34%.
E) The probability of having either feature (81%) doesn't equal the probability of having just one
feature (60% and 55%).
(Essay)
4.9/5  (29)
(29)
Is there evidence of an association between GPA and ACT score? Test an appropriate
hypothesis and state your conclusion in the proper context.
(Essay)
4.8/5  (34)
(34)
For a class project, students tested four different brands of laundry detergent (1, 2, 3, 4) in
three different water temperatures (hot, warm, cold) to see whether their were any
differences in how well the detergents could clean clothes. The students took 36 identical
pieces of cloth and made them dirty by staining them with coffee, dirt, and grass. The 36
pieces were randomly assigned to the 12 combinations of detergent and temperature so
that each combination had 3 replicates. After washing, the students rated how clean the
clothes were from 0 (no change) to 20 (completely spotless). The two factor ANOVA table
is shown below along with an interaction plot and residual plots. Source df Sums of Squares Mean Square F-ratio P-value Detergent 3 38.972 12.9907 3.966 0.0171 Temp 2 181.056 90.5278 27.634 <0.0001 Error 30 98.278 3.2759 Total 35 318.306
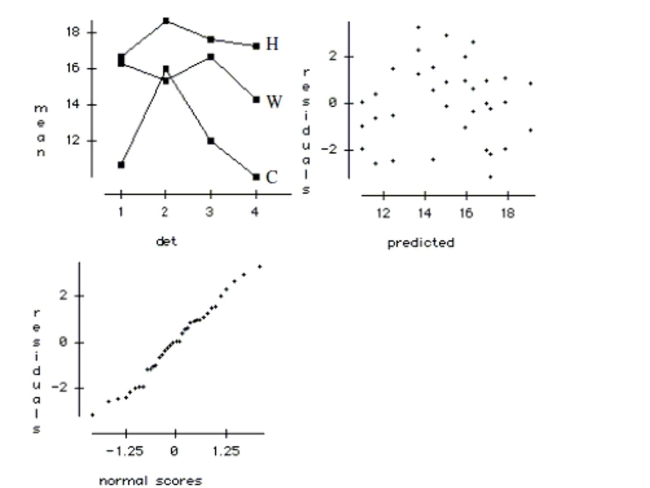 a. Write the hypotheses tested by the Detergent F-ratio. Test the hypotheses and explain
your conclusion in the context of the problem.
b. Write the hypotheses tested by the Temp F-ratio. Test the hypotheses and explain your
conclusion in the context of the problem.
c. Check the conditions required for the ANOVA analysis.
a. Write the hypotheses tested by the Detergent F-ratio. Test the hypotheses and explain
your conclusion in the context of the problem.
b. Write the hypotheses tested by the Temp F-ratio. Test the hypotheses and explain your
conclusion in the context of the problem.
c. Check the conditions required for the ANOVA analysis.
(Essay)
4.9/5  (45)
(45)
Describe how you will use a random number table to conduct this simulation.
(Essay)
4.8/5  (43)
(43)
How many times should the restaurant expect to have to get this freezer repaired over the
three-year term of the lease?
(Essay)
4.9/5  (37)
(37)
A regression model examining the amount of distance a long distance runner runs (in miles) to
Predict the amount of fluid the runner drinks (ounces) has a slope of 4.6. Which interpretation is
Appropriate?
(Multiple Choice)
4.8/5  (28)
(28)
A regression model examining the amount of weight a football player can bench press found that
10 cm differences in chest size are associated with 8 kg differences in weight pressed. Which is
True?
I. The correlation between chest size and weight pressed is
II. As a player gets stronger and presses more weight his chest will get bigger.
III. A positive residual means that the player pressed more than predicted.
(Multiple Choice)
4.8/5  (39)
(39)
The farmer with 35 had 15,400 oranges; find the value of his residual. Show your work.
(Essay)
4.9/5  (32)
(32)
Showing 781 - 792 of 792
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)