Exam 13: Vector Calculus
Exam 1: Functions and Models118 Questions
Exam 2: Limits and Derivatives127 Questions
Exam 3: Differentiation Rules248 Questions
Exam 4: Applications of Differentiation273 Questions
Exam 5: Integrals239 Questions
Exam 6: Applications of Integration189 Questions
Exam 7: Differential Equations154 Questions
Exam 8: Infinite Sequences and Series341 Questions
Exam 9: Vectors and the Geometry of Space269 Questions
Exam 10: Vector Functions111 Questions
Exam 11: Partial Derivatives294 Questions
Exam 12: Multiple Integrals270 Questions
Exam 13: Vector Calculus240 Questions
Select questions type
Each vector field F graphed below is shown in the xy-plane and looks the same in all other horizontal planes. Is div F at the point P positive, negative or zero? Is curl F at the point P equal to 0? Explain.(a) 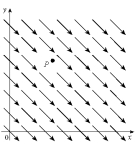 (b)
(b) 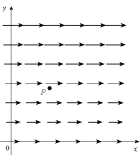 (c)
(c) 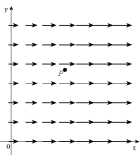
(Essay)
4.8/5  (41)
(41)
Determine whether is conservative and if so, find a potential function.
(Short Answer)
4.8/5  (35)
(35)
Evaluate the line integral , where consists of line segments from to , from to , and from to .
(Short Answer)
5.0/5  (36)
(36)
Evaluate the line integral , where C is the upper half of the circle from to .
(Short Answer)
4.7/5  (39)
(39)
Evaluate the line integral where is the curve from to , to to , then to .
(Short Answer)
4.9/5  (24)
(24)
Let and let S be the boundary surface of the solid . Evaluate the surface integral .
(Short Answer)
4.7/5  (35)
(35)
Let and let S be the boundary surface of the solid . Evaluate the surface integral .
(Multiple Choice)
4.9/5  (29)
(29)
Find the value of the gradient vector field of the function at the point .
(Multiple Choice)
4.7/5  (38)
(38)
Let and let S be the boundary surface of the solid . Evaluate the surface integral .
(Short Answer)
4.8/5  (38)
(38)
What value of the constant a makes the vector field conservative?
(Multiple Choice)
4.7/5  (34)
(34)
Evaluate , where and S is the part of the surface below the plane , with upward orientation.
(Short Answer)
4.7/5  (35)
(35)
Find the mass and center of mass of a thin wire in the shape of a quarter-circle , , if the density function is .
(Essay)
4.8/5  (37)
(37)
Evaluate the flux of the vector field through the plane region with the given orientation as shown below. 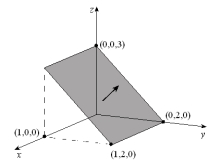
(Short Answer)
4.8/5  (44)
(44)
Find the flux of across the surface of the solid bounded by the paraboloid and the plane.
(Short Answer)
4.9/5  (43)
(43)
Showing 41 - 60 of 240
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)