Exam 13: Vector Calculus
Exam 1: Functions and Models118 Questions
Exam 2: Limits and Derivatives127 Questions
Exam 3: Differentiation Rules248 Questions
Exam 4: Applications of Differentiation273 Questions
Exam 5: Integrals239 Questions
Exam 6: Applications of Integration189 Questions
Exam 7: Differential Equations154 Questions
Exam 8: Infinite Sequences and Series341 Questions
Exam 9: Vectors and the Geometry of Space269 Questions
Exam 10: Vector Functions111 Questions
Exam 11: Partial Derivatives294 Questions
Exam 12: Multiple Integrals270 Questions
Exam 13: Vector Calculus240 Questions
Select questions type
Find the work done by the force field on a particle that moves along the circle C: .
(Short Answer)
4.7/5  (38)
(38)
Let . Evaluate the line integral along the elliptical path .
(Multiple Choice)
4.7/5  (31)
(31)
Let . Find the value of the curl of F at the point (1,1,3).
(Multiple Choice)
4.9/5  (35)
(35)
Determine whether is conservative and if so, find a potential function.
(Essay)
4.7/5  (39)
(39)
For what value of the constant is the vector field conservative?
(Multiple Choice)
4.8/5  (42)
(42)
Find a formula for the vector field graphed below. (There are many possible answers.) 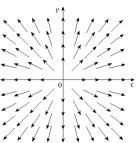
(Essay)
4.8/5  (39)
(39)
Evaluate the line integral :
(a) if is the line segment from to .(b) if is the line segment from to .
(Short Answer)
4.9/5  (36)
(36)
Use the Divergence Theorem to evaluate where and S is the surface of the cylinder , bounded by the planes and .
(Multiple Choice)
4.9/5  (41)
(41)
Let . Note that . Evaluate the line integral where C is the curve , .
(Short Answer)
4.7/5  (34)
(34)
Find a function f such that and use it to evaluate along the curve C. C is the arc of the curve from to .
(Essay)
4.8/5  (40)
(40)
Evaluate the line integral , where and the curve is given by the vector function .
(Short Answer)
4.8/5  (42)
(42)
Evaluate where C is the positively-oriented boundary of the half disk D: .
(Short Answer)
4.7/5  (33)
(33)
Find the work done by the force F in moving an object from to along the path given by ..
(Short Answer)
4.9/5  (42)
(42)
Use Green's Theorem to find the area of the region formed by the intersection of and .
(Short Answer)
4.8/5  (40)
(40)
Let . Evaluate the line integral along the elliptical path .
(Multiple Choice)
4.8/5  (41)
(41)
Showing 161 - 180 of 240
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)