Exam 11: Partial Derivatives
Exam 1: Functions and Models118 Questions
Exam 2: Limits and Derivatives127 Questions
Exam 3: Differentiation Rules248 Questions
Exam 4: Applications of Differentiation273 Questions
Exam 5: Integrals239 Questions
Exam 6: Applications of Integration189 Questions
Exam 7: Differential Equations154 Questions
Exam 8: Infinite Sequences and Series341 Questions
Exam 9: Vectors and the Geometry of Space269 Questions
Exam 10: Vector Functions111 Questions
Exam 11: Partial Derivatives294 Questions
Exam 12: Multiple Integrals270 Questions
Exam 13: Vector Calculus240 Questions
Select questions type
Let .(a) Sketch the intersection of and in the -plane.(b) Sketch the intersection of and in the -plane.(c) Sketch the intersection of and in the -plane.(d) Sketch the graph of in .
(Essay)
4.8/5  (30)
(30)
Let and let .(a) Find the directional derivative at in the direction of .(b) In what direction does increase most rapidly?
(c) What is the maximum rate of change of at the point ?
(Essay)
4.9/5  (36)
(36)
Describe the vertical traces and and the horizontal traces for the function .
(Essay)
4.9/5  (38)
(38)
Let . Find the directional derivative of at in the direction of the vector .
(Short Answer)
4.9/5  (43)
(43)
How many third-order partial derivatives does a function have?
(Multiple Choice)
4.9/5  (37)
(37)
If is a function of and , and is a function of , then indirectly depends only on : . Use the Chain Rule to write an expression for in terms of and .
(Essay)
4.9/5  (39)
(39)
Find the local maximum and minimum values and saddle points of the function .
(Essay)
4.8/5  (34)
(34)
Use the level curves of shown below to estimate the critical points of . Indicate whether has a saddle point or a local maximum or minimum at each of those points. 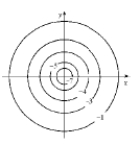
(Essay)
4.8/5  (38)
(38)
Find an equation of the tangent plane to the parametric surface at the point .
(Essay)
4.8/5  (30)
(30)
Let Does this function have a limit at the origin?
If so, prove it. If not, demonstrate why not.
(Essay)
4.9/5  (31)
(31)
If , find the values for which , and then find an equation of the plane tangent to the graph of at .
(Essay)
4.7/5  (36)
(36)
Showing 41 - 60 of 294
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)