Exam 11: Partial Derivatives
Exam 1: Functions and Models118 Questions
Exam 2: Limits and Derivatives127 Questions
Exam 3: Differentiation Rules248 Questions
Exam 4: Applications of Differentiation273 Questions
Exam 5: Integrals239 Questions
Exam 6: Applications of Integration189 Questions
Exam 7: Differential Equations154 Questions
Exam 8: Infinite Sequences and Series341 Questions
Exam 9: Vectors and the Geometry of Space269 Questions
Exam 10: Vector Functions111 Questions
Exam 11: Partial Derivatives294 Questions
Exam 12: Multiple Integrals270 Questions
Exam 13: Vector Calculus240 Questions
Select questions type
Find the directional derivative of the function at the point in the direction .
(Multiple Choice)
4.8/5  (37)
(37)
Find the direction of maximum increase of the function at the point .
(Multiple Choice)
4.8/5  (44)
(44)
Let .(a) Evaluate .(b) Sketch the domain of .(c) What is the range of the function ?
(Essay)
4.9/5  (35)
(35)
Let . Find the rate of change of at the point in the direction where is a unit vector making an angle with .
(Essay)
4.8/5  (36)
(36)
The level curves of are sketched below. 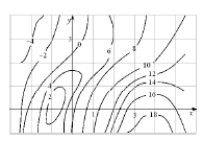 (a) Find (b) Find (c) Sketch the gradient vector .
(a) Find (b) Find (c) Sketch the gradient vector .
(Essay)
4.9/5  (33)
(33)
Let . Find the rate of change of at the point in the direction where is a unit vector making an angle with .
(Essay)
5.0/5  (38)
(38)
Given that the directional derivative of at the point in the direction of is and that , find .
(Short Answer)
4.9/5  (28)
(28)
Find an equation of the tangent plant to the surface at the point .
(Multiple Choice)
4.8/5  (32)
(32)
Let . Find the rate of change of at in the direction from toward .
(Short Answer)
4.8/5  (33)
(33)
Suppose you want to give a closed cylindrical tank of radius 20 feet and height 15 feet a cost of paint 0.01 inch thick. Use the differential of the volume of the tank to estimate how many gallons of paint will be required. (1 gallon is approximately 231 cubic inches.)
(Short Answer)
4.8/5  (47)
(47)
Let and let be the curve with the equation , where is a constant. The value of the limit of as approaches along is
(Multiple Choice)
4.7/5  (43)
(43)
Showing 81 - 100 of 294
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)