Exam 11: Partial Derivatives
Exam 1: Functions and Models118 Questions
Exam 2: Limits and Derivatives127 Questions
Exam 3: Differentiation Rules248 Questions
Exam 4: Applications of Differentiation273 Questions
Exam 5: Integrals239 Questions
Exam 6: Applications of Integration189 Questions
Exam 7: Differential Equations154 Questions
Exam 8: Infinite Sequences and Series341 Questions
Exam 9: Vectors and the Geometry of Space269 Questions
Exam 10: Vector Functions111 Questions
Exam 11: Partial Derivatives294 Questions
Exam 12: Multiple Integrals270 Questions
Exam 13: Vector Calculus240 Questions
Select questions type
Let .(a) In which direction does increase most rapidly at the point ?
(b) What is the maximum rate of change of at the point ?
(c) Find a unit vector such that at .
(Essay)
4.8/5  (34)
(34)
Find the linear approximation to the function at and use it to approximate .
(Essay)
4.9/5  (42)
(42)
The level curves of a function and a curve with equation ( constant) are given below. Estimate the point where has a maximum value and the point where has a minimum value, subject to the constraint that . Indicate your answer in the figure. 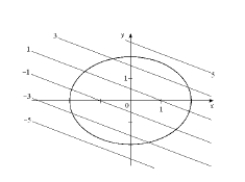
(Essay)
4.9/5  (37)
(37)
A right triangle as leg wit length 4, leg with length 3, and hypotenuse with length 5. Use a total differential to approximate the length of the hypotenuse if leg had length 4.2 and leg had length 2.9.
(Short Answer)
4.9/5  (36)
(36)
Let , and let and be functions of and with , , and at . Find when .
(Multiple Choice)
4.9/5  (33)
(33)
Use the method of Lagrange multipliers to find points on the surface of where the function has
(a) a minimum
(b) a maximum.
(Essay)
4.9/5  (34)
(34)
Use differentials to estimate the amount of metal in a closed cylindrical can that is 10 cm high and 4 cm in diameter if the metal in the wall is 0.05 cm thick and the metal in the top and bottom is 0.1 cm thick.
(Multiple Choice)
4.9/5  (40)
(40)
If , find the partial derivative of with respect to and the partial derivative with respect to , both at the point .
(Essay)
4.7/5  (34)
(34)
Consider the equation .(a) Sketch this surface. 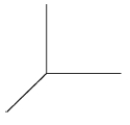 (b) Find an equation of the tangent plane to the surface at the point .(c) Find a symmetric equation of the line perpendicular to the tangent plane at the point .
(b) Find an equation of the tangent plane to the surface at the point .(c) Find a symmetric equation of the line perpendicular to the tangent plane at the point .
(Essay)
4.9/5  (46)
(46)
A bug is crawling on the surface . When he reaches the point he wants to avoid vertical change. In which direction should he head? (He wants the directional derivative in the -direction to be zero.)
(Essay)
4.8/5  (31)
(31)
If is a function of and , and is a function of , then indirectly depends only on . If and , calculate .
(Essay)
4.8/5  (42)
(42)
Consider the surface given by . Find an equation for the tangent plane to the surface at the point . Also, find parametric equations for the normal line to the surface at the point
(Essay)
4.8/5  (42)
(42)
Determine if is everywhere continuous, and if not, locate the point(s) of discontinuity.
(Essay)
4.8/5  (33)
(33)
Showing 221 - 240 of 294
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)