Exam 11: Partial Derivatives
Exam 1: Functions and Models118 Questions
Exam 2: Limits and Derivatives127 Questions
Exam 3: Differentiation Rules248 Questions
Exam 4: Applications of Differentiation273 Questions
Exam 5: Integrals239 Questions
Exam 6: Applications of Integration189 Questions
Exam 7: Differential Equations154 Questions
Exam 8: Infinite Sequences and Series341 Questions
Exam 9: Vectors and the Geometry of Space269 Questions
Exam 10: Vector Functions111 Questions
Exam 11: Partial Derivatives294 Questions
Exam 12: Multiple Integrals270 Questions
Exam 13: Vector Calculus240 Questions
Select questions type
Find the maximum and minimum values of the function on the ellipse given by the equation .
(Essay)
4.8/5  (46)
(46)
The function has one critical point. Determine its location and type.
(Multiple Choice)
4.8/5  (24)
(24)
In using Lagrange multipliers to minimize the function subject to the constraint that , what is the value of the multiplier ?
(Multiple Choice)
4.8/5  (33)
(33)
The dimensions of a closed rectangular box are measured to be 60 cm, 40 cm, and 30 cm. The ruler that is used has a possible error in measurement of at most 0.1 cm. Use differentials to estimate the maximum error in the calculated volume of the box.
(Short Answer)
4.8/5  (43)
(43)
Use the level curves of shown below to estimate the critical points of . Indicate whether has a saddle point or a local maximum or minimum at each of those points. 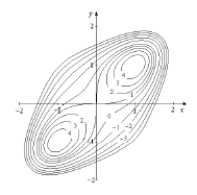
(Essay)
4.8/5  (40)
(40)
Find the directions in which the directional derivative of at the point has the value 1.
(Short Answer)
4.7/5  (41)
(41)
The graph of level curves of is given. Find a possible formula for and sketch the surface . 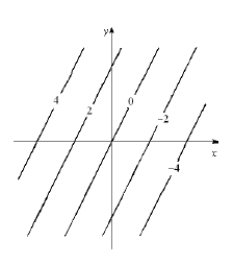
(Essay)
4.9/5  (38)
(38)
Find the absolute maximum and minimum value of on the square region with vertices , , , and .
(Essay)
4.9/5  (43)
(43)
Showing 161 - 180 of 294
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)