Exam 5: Applications of Derivatives
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
Solve the problem.
-A long strip of sheet metal 12 inches wide is to be made into a small trough by turning up two sides at right angles to the base. If the trough is to have maximum capacity, how many inches should be turned up on each
Side?
(Multiple Choice)
4.9/5  (38)
(38)
Solve the problem.
-Use Newton's method to estimate the solution of the equation . Start with . Then, in each case find .
(Essay)
4.8/5  (38)
(38)
Estimate the limit by graphing the function for an appropriate domain. Confirm your estimate by using L'Hopital's rule.
Show each step of your calculation.
-Which one is correct, and which one is wrong? Give reasons for your answers.
(a)
(b)
(Essay)
4.9/5  (39)
(39)
Graph the function, then find the extreme values of the function on the interval and indicate where they occur.
- on the interval
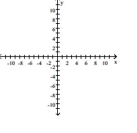
(Multiple Choice)
4.7/5  (36)
(36)
Plot the zeros of the given polynomial on the number line together with the zeros of the first derivative.
-
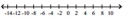
(Multiple Choice)
4.9/5  (28)
(28)
Use differentiation to determine whether the integral formula is correct.
-
(True/False)
4.9/5  (42)
(42)
Solve the problem.
-Find the inflection points (if any) on the graph of the function and the coordinates of the points on the graph whe function has a local maximum or local minimum value. Then graph the function in a region large enough to shor these points simultaneously. Add to your picture the graphs of the function's first and second derivatives.
(Essay)
4.8/5  (31)
(31)
Find the largest open interval where the function is changing as requested.
-Decreasing
(Multiple Choice)
4.7/5  (36)
(36)
Find the extreme values of the function and where they occur.
-
(Multiple Choice)
4.8/5  (39)
(39)
Using the derivative of f(x) given below, determine the critical points of f(x).
-f(x) = (x + 9)(x + 8)
(Multiple Choice)
4.9/5  (46)
(46)
Answer the problem.
-Use the following function and a graphing calculator to answer the questions.
a). Plot the function over the interval to see its general behavior there. Sketch the graph below.
![Answer the problem. -Use the following function and a graphing calculator to answer the questions. f ( x ) = x ^ { 4 } - 5 x ^ { 2 } + 4 x + 3 , [ - 0.5,1.8 ] a). Plot the function over the interval to see its general behavior there. Sketch the graph below. b). Find the interior points where f = 0 (you may need to use the numerical equation solver to approximate a solution). You may wish to plot f as well. List the points as ordered pairs (x, y). c). Find the interior points where f does not exist. List the points as ordered pairs (x, y). d). Evaluate the function at the endpoints and list these points as ordered pairs (x, y). e). Find the function's absolute extreme values on the interval and identify where they occur.](https://storage.examlex.com/TB6591/11ecd900_9094_c932_8f2a_6538229f3a21_TB6591_11.jpg) b). Find the interior points where f = 0 (you may need to use the numerical equation solver to approximate a solution). You may wish to plot f as well. List the points as ordered pairs (x, y).
c). Find the interior points where f does not exist. List the points as ordered pairs (x, y).
d). Evaluate the function at the endpoints and list these points as ordered pairs (x, y).
e). Find the function's absolute extreme values on the interval and identify where they occur.
b). Find the interior points where f = 0 (you may need to use the numerical equation solver to approximate a solution). You may wish to plot f as well. List the points as ordered pairs (x, y).
c). Find the interior points where f does not exist. List the points as ordered pairs (x, y).
d). Evaluate the function at the endpoints and list these points as ordered pairs (x, y).
e). Find the function's absolute extreme values on the interval and identify where they occur.
(Essay)
4.9/5  (31)
(31)
Showing 261 - 280 of 412
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)