Exam 5: Applications of Derivatives
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
Find the extreme values of the function and where they occur.
-
(Multiple Choice)
5.0/5  (32)
(32)
Find a value of c that makes the function continuous at the given value of x. If it is impossible, state this.
-
(Multiple Choice)
4.9/5  (32)
(32)
Solve the problem.
-A private shipping company will accept a box for domestic shipment only if the sum of its length and girth (distance around) does not exceed 90 in. What dimensions will give a box with a square end the largest possible
Volume? 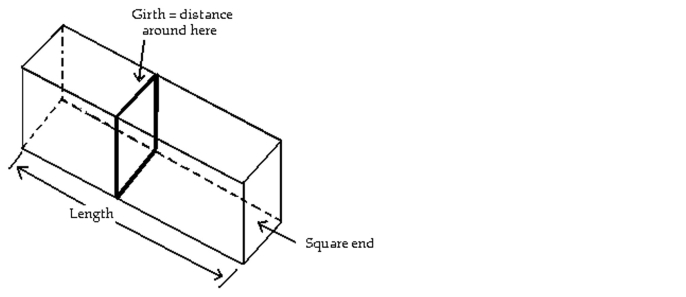
(Multiple Choice)
4.9/5  (38)
(38)
Solve the problem.
-Use Newton's method to estimate the solutions of the equation . Start with for the right-hand solution and with for the solution on the left. Then, in each case find .
(Essay)
4.9/5  (36)
(36)
Estimate the limit by graphing the function for an appropriate domain. Confirm your estimate by using L'Hopital's rule.
Show each step of your calculation.
-Find the error in the following incorrect application of L'Hôpital's Rule. .
(Essay)
4.9/5  (32)
(32)
Plot the zeros of the given polynomial on the number line together with the zeros of the first derivative.
-

(Multiple Choice)
4.9/5  (37)
(37)
Solve the problem.
-Show that if , applying Newton's method to
leads to if and to if when .
(Essay)
4.8/5  (35)
(35)
Solve the problem.
-Find the inflection points (if any) on the graph of the function and the coordinates of the points on the graph whe function has a local maximum or local minimum value. Then graph the function in a region large enough to shor these points simultaneously. Add to your picture the graphs of the function's first and second derivatives.
(Essay)
4.9/5  (38)
(38)
Sketch the graph and show all local extrema and inflection points.
-
(Multiple Choice)
5.0/5  (31)
(31)
Solve the problem.
-How close does the semicircle come to the point ?
(Multiple Choice)
4.9/5  (39)
(39)
Using the derivative of f(x) given below, determine the intervals on which f(x) is increasing or decreasing.
-
(Multiple Choice)
4.8/5  (31)
(31)
Solve the problem.
-The positions of two particles on the s-axis are and , with and in meters and in seconds.
At what time(s) in the interval do the particles meet?
(Multiple Choice)
4.8/5  (44)
(44)
Solve the problem.
-A window is in the form of a rectangle surmounted by a semicircle. The rectangle is of clear glass, whereas the semicircle is of tinted glass that transmits only one-fourth as much light per unit area as clear glass does. The total perimeter is fixed. Find the proportions of the window that will admit the most light. Neglect the thickness of the frame.
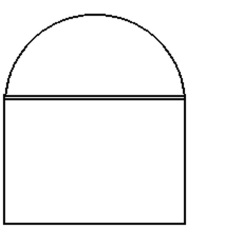
(Multiple Choice)
4.9/5  (38)
(38)
Showing 361 - 380 of 412
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)