Exam 5: Applications of Derivatives
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
Solve the problem.
-Sketch a continuous curve y = f(x) with the following properties:
f(2) = 3; f (x) > 0 for x > 4; and f (x) < 0 for x < 4 .
(Essay)
4.8/5  (28)
(28)
Find the largest open interval where the function is changing as requested.
-Increasing
(Multiple Choice)
4.8/5  (50)
(50)
Solve the problem.
-Given the velocity and initial position of a body moving along a coordinate line at time t, find the body's positior .
(Multiple Choice)
4.7/5  (28)
(28)
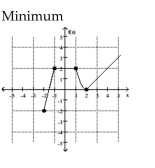
Find the location of the indicated absolute extremum for the function.
-
(Multiple Choice)
4.9/5  (37)
(37)
Find the extreme values of the function and where they occur.
-
(Multiple Choice)
4.9/5  (36)
(36)
Use the maximum/minimum finder on a graphing calculator to determine the approximate location of all local extrema.
-
(Multiple Choice)
4.7/5  (38)
(38)
Solve the problem.
-Find the graph that matches the given table.
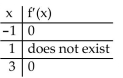
(Multiple Choice)
4.8/5  (38)
(38)
Identify the function's local and absolute extreme values, if any, saying where they occur.
-
(Multiple Choice)
4.9/5  (44)
(44)
Find the absolute extreme values of the function on the interval.
-
(Multiple Choice)
4.8/5  (44)
(44)
L'Hopital's rule does not help with the given limit. Find the limit some other way.
-
(Multiple Choice)
4.9/5  (38)
(38)
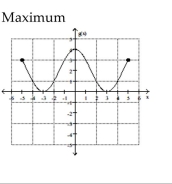
Find the location of the indicated absolute extremum for the function.
-
(Multiple Choice)
4.9/5  (36)
(36)
L'Hopital's rule does not help with the given limit. Find the limit some other way.
-
(Multiple Choice)
4.8/5  (37)
(37)
Solve the problem.
-Sketch a smooth curve through the origin with the following properties: for for ; approaches 0 as approaches ; and approaches 0 as approaches .
(Essay)
4.8/5  (33)
(33)
Solve the problem.
-You are driving along a highway at a steady when you see a deer ahead and slam on the brakes. What constant deceleration is required to stop your car in ?
(Multiple Choice)
4.9/5  (33)
(33)
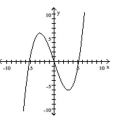
Use the graph of the function f(x) to locate the local extrema and identify the intervals where the function is concave up
and concave down.
-
(Multiple Choice)
4.9/5  (36)
(36)
Showing 21 - 40 of 412
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)