Exam 5: Applications of Derivatives
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
Use differentiation to determine whether the integral formula is correct.
-
(True/False)
4.9/5  (36)
(36)
Solve the problem.
-The graphs below show the first and second derivatives of a function . Select a possible graph that passe through the point .
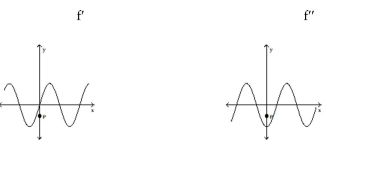
(Multiple Choice)
4.9/5  (39)
(39)
Solve the problem.
-Use Newton's method to find the value of for which . Find the answer correct to five decimal places.
(Multiple Choice)
4.8/5  (39)
(39)
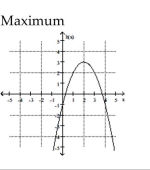
Find the location of the indicated absolute extremum for the function.
-
(Multiple Choice)
4.9/5  (35)
(35)
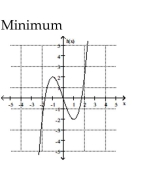
Find the location of the indicated absolute extremum for the function.
-
(Multiple Choice)
4.7/5  (41)
(41)
Answer the question.
-A marathoner ran the 26.2 mile New York City Marathon in 2.8 hrs. Did the runner ever exceed a speed of 9
miles per hour?
(Essay)
4.9/5  (42)
(42)
Graph the rational function.
-\9\begin{array} { c }
y = \frac { x ^ { 2 } + x - 42 } { x ^ { 2 } - x - 56 } \\
\end{array}\)
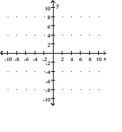
(Multiple Choice)
4.8/5  (43)
(43)
Solve the problem.
-At about what velocity do you enter the water if you jump from a 15 meter cliff? (Use .)
(Multiple Choice)
4.9/5  (45)
(45)
Show that the function has exactly one zero in the given interval.
-
(Essay)
4.8/5  (38)
(38)
Find a value of c that makes the function continuous at the given value of x. If it is impossible, state this.
-
(Multiple Choice)
4.9/5  (27)
(27)
Answer the problem.
-Let
(a) Does exist?
(b) Show that the only local extreme value of occurs at .
(c) Does the result of (b) contradict the Extreme Value Theorem?
(d) Repeat parts (a) and (b) for .
Give reasons for your answers.
(Essay)
4.8/5  (32)
(32)
Solve the problem.
-Suppose Newton's Method is used with an initial guess that lies at a critical point . What happens to and later approximations? Give reasons for your answer.
(Essay)
4.9/5  (30)
(30)
Solve the problem.
-Write down the first four approximations to the solution of the equation using Newton's method with an initial estimate of .
(Essay)
4.8/5  (31)
(31)
Find a value of c that makes the function continuous at the given value of x. If it is impossible, state this.
-
(Multiple Choice)
4.8/5  (39)
(39)
Solve the problem.
-Given the velocity and initial position of a body moving along a coordinate line at time , find the body's position
(Multiple Choice)
4.8/5  (38)
(38)
Showing 381 - 400 of 412
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)