Exam 5: Applications of Derivatives
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
Solve the problem.
-Explain why the following four statements ask for the same information.
(i) Find the roots of
(ii) Find the -coordinates of the intersections of the curve with the line .
(iii) Find the -coordinates of the points where the curve crosses the horizontal line .
(iv) Find the values of where the derivative of equals zero.
(Essay)
4.9/5  (35)
(35)
Provide an appropriate response.
-Find the absolute maximum and minimum values of on .
(Multiple Choice)
4.9/5  (33)
(33)
Find the value or values of that satisfy the equation in the conclusion of the Mean Value Theorem for the function and interval.
-
Round to the nearest thousandth.
(Multiple Choice)
4.9/5  (54)
(54)
Find the absolute extreme values of the function on the interval.
-
(Multiple Choice)
4.7/5  (37)
(37)
Solve the problem.
-Use Newton's method to estimate the one real solution of the equation . Start with . Then, in each case find .
(Essay)
4.8/5  (34)
(34)
Use Newton's method to estimate the requested solution of the equation. Start with given value of x0 and then give x2 as
the estimated solution.
-
(Multiple Choice)
4.8/5  (40)
(40)
Find the function with the given derivative whose graph passes through the point P.
-
(Multiple Choice)
4.8/5  (42)
(42)
Solve the problem.
-Select an appropriate graph of a twice-differentiable function that passes through the points , and , and whose first two derivatives have the following sign patterns.
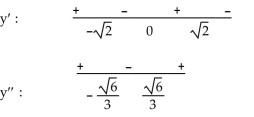
(Multiple Choice)
4.7/5  (35)
(35)
Solve the problem.
-Can anything be said about the graph of a function y = f(x) that has a second derivative that is always equal to zero? Give reasons for your answer.
(Essay)
4.8/5  (36)
(36)
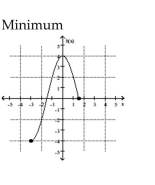
Find the location of the indicated absolute extremum for the function.
-
(Multiple Choice)
4.9/5  (35)
(35)
Use Newton's method to estimate the requested solution of the equation. Start with given value of x0 and then give x2 as
the estimated solution.
-
(Multiple Choice)
4.8/5  (37)
(37)
Find the extrema of the function on the given interval, and say where they occur.
-
(Multiple Choice)
4.9/5  (34)
(34)
Identify the function's local and absolute extreme values, if any, saying where they occur.
-
(Multiple Choice)
4.8/5  (48)
(48)
Graph the equation. Include the coordinates of any local and absolute extreme points and inflection points.
-y
(Multiple Choice)
4.8/5  (42)
(42)
Solve the problem.
-Use Newton's method to estimate the solutions of the equation . Start with for the right-hand solution and with for the solution on the left. Then, in each case find .
(Essay)
4.7/5  (40)
(40)
Solve the problem.
-A manufacturer uses raw materials to produce p products each day. Suppose that each delivery of a particular
material is $d, whereas the storage of that material is x dollars per unit stored per day. (One unit is the amount
required to produce one product). How much should be delivered every x days to minimize the average daily
cost in the production cycle between deliveries?
(Essay)
5.0/5  (38)
(38)
Solve the problem.
-Marcus Tool and Die Company produces a specialized milling tool designed specifically for machining ceramic components. Each milling tool sells for , so the company's revenue in dollars for units sold is . The company's cost in dollars to produce tools can be modeled as . Use Newton's method to find the break-even point for the company (that is, find such that ). Use as your initial guess and show all your work.
(Essay)
4.7/5  (43)
(43)
Graph the equation. Include the coordinates of any local and absolute extreme points and inflection points.
-
(Multiple Choice)
4.9/5  (42)
(42)
Graph the equation. Include the coordinates of any local and absolute extreme points and inflection points.
-y
(Multiple Choice)
4.7/5  (25)
(25)
Answer each question appropriately.
-Suppose the velocity of a body moving along the s-axis is .
Find the body's displacement over the time interval from to given that when .
(Multiple Choice)
4.7/5  (30)
(30)
Showing 281 - 300 of 412
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)