Exam 5: Applications of Derivatives
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
Solve the problem.
-Use Newton's method to find the positive fourth root of 5 by solving the equation . Start with and find .
(Essay)
4.9/5  (31)
(31)
Estimate the limit by graphing the function for an appropriate domain. Confirm your estimate by using L'Hopital's rule.
Show each step of your calculation.
-
(Essay)
4.7/5  (39)
(39)
Estimate the limit by graphing the function for an appropriate domain. Confirm your estimate by using L'Hopital's rule.
Show each step of your calculation.
-Given that , find the maximum value, if any, of .
(Multiple Choice)
4.9/5  (39)
(39)
Solve the problem.
-A company is constructing an open-top, square-based, rectangular metal tank that will have a volume of . What dimensions yield the minimum surface area? Round to the nearest tenth, if necessary.
(Multiple Choice)
4.7/5  (37)
(37)
Identify the function's extreme values in the given domain, and say where they are assumed. Tell which of the extreme
values, if any, are absolute.
-
(Multiple Choice)
4.7/5  (29)
(29)
Find the value or values of that satisfy the equation in the conclusion of the Mean Value Theorem for the function and interval.
-
(Multiple Choice)
4.8/5  (36)
(36)
Solve the problem.
-The stiffness of a rectangular beam is proportional to its width times the cube of its depth. Find the dimensions of the stiffest beam than can be cut from a 13-in.-diameter cylindrical log. (Round answers to the nearest tenth.)
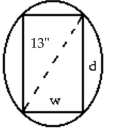
(Multiple Choice)
4.9/5  (31)
(31)
Solve the problem.
-Use Newton's method to find the value of for which . Find the answer correct to five decimal places.
(Multiple Choice)
4.9/5  (33)
(33)
L'Hopital's rule does not help with the given limit. Find the limit some other way.
-
(Multiple Choice)
4.8/5  (42)
(42)
Use the maximum/minimum finder on a graphing calculator to determine the approximate location of all local extrema.
-
(Multiple Choice)
4.7/5  (42)
(42)
Find the absolute extreme values of the function on the interval.
-
(Multiple Choice)
4.9/5  (34)
(34)
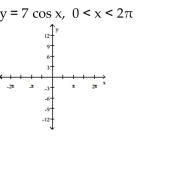
Sketch the graph of the function and determine whether it has any absolute extreme values on its domain.
-
(Multiple Choice)
4.9/5  (35)
(35)
Showing 141 - 160 of 412
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)