Exam 5: Applications of Derivatives
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
Solve the problem.
-Suppose that is the cost of manufacturing items. Find a production level that will minimize the average cost of making items.
(Multiple Choice)
4.9/5  (36)
(36)
Solve the problem.
-Given the acceleration, initial velocity, and initial position of a body moving along a coordinate line at time t, find the body's position at time t.
A = 16 cos 4t, v(0) = 8, s(0) = 3
(Multiple Choice)
4.8/5  (39)
(39)
Find the absolute extreme values of the function on the interval.
-
(Multiple Choice)
4.8/5  (38)
(38)
Solve the problem.
-The strength of a rectangular wooden beam is proportional to its width times the square of its depth. Find the dimensions of the strongest beam that can be cut from a 10 -in.-diameter cylindrical log. (Round answers to the nearest tenth.)
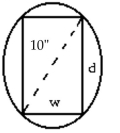
(Multiple Choice)
4.7/5  (35)
(35)
Use the maximum/minimum finder on a graphing calculator to determine the approximate location of all local extrema.
-
(Multiple Choice)
4.8/5  (31)
(31)
Use Newton's method to estimate the requested solution of the equation. Start with given value of x0 and then give x2 as
the estimated solution.
-
(Multiple Choice)
4.8/5  (36)
(36)
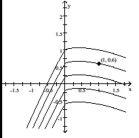
The graph below shows solution curves of a differential equation. Find an equation for the curve through the given point.
-
(Multiple Choice)
5.0/5  (33)
(33)
Find the absolute extreme values of the function on the interval.
-
(Multiple Choice)
4.9/5  (36)
(36)
Find the function with the given derivative whose graph passes through the point P.
-
(Multiple Choice)
4.8/5  (36)
(36)
Find the absolute extreme values of the function on the interval.
-
(Multiple Choice)
4.8/5  (35)
(35)
Find the function with the given derivative whose graph passes through the point P.
-
(Multiple Choice)
4.8/5  (38)
(38)
Solve the problem.
-Suppose is the cost of manufacturing items. Find a production level that will minimize the average cost of making items.
(Multiple Choice)
4.8/5  (40)
(40)
Use the maximum/minimum finder on a graphing calculator to determine the approximate location of all local extrema.
-
(Multiple Choice)
4.8/5  (45)
(45)
Showing 161 - 180 of 412
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)