Exam 5: Applications of Derivatives
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
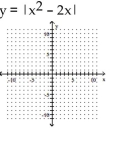
Sketch the graph and show all local extrema and inflection points.
-
(Multiple Choice)
4.8/5  (39)
(39)
Estimate the limit by graphing the function for an appropriate domain. Confirm your estimate by using L'Hopital's rule.
Show each step of your calculation.
-
(Essay)
4.9/5  (40)
(40)
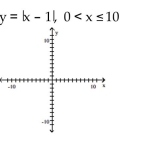
Sketch the graph of the function and determine whether it has any absolute extreme values on its domain.
-
(Multiple Choice)
4.8/5  (27)
(27)
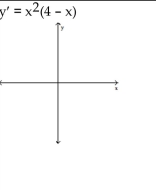
For the given expression y, find y'' and sketch the general shape of the graph of y = f(x).
-
(Multiple Choice)
4.8/5  (39)
(39)
Solve the problem.
-A rocket lifts off the surface of Earth with a constant acceleration of . How fast will the rocket be going minutes later?
(Multiple Choice)
4.9/5  (31)
(31)
Use the maximum/minimum finder on a graphing calculator to determine the approximate location of all local extrema.
-
(Multiple Choice)
4.9/5  (28)
(28)
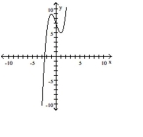
Use the graph of the function f(x) to locate the local extrema and identify the intervals where the function is concave up
and concave down.
-
(Multiple Choice)
5.0/5  (40)
(40)
Solve the problem.
-The graphs below show the first and second derivatives of a function . Select a possible graph that passe through the point .
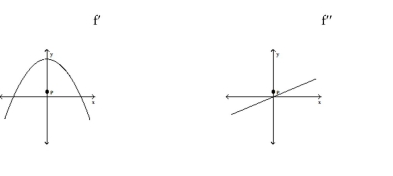
(Multiple Choice)
4.8/5  (39)
(39)
Find the absolute extreme values of the function on the interval.
-
(Multiple Choice)
4.8/5  (33)
(33)
Find the extrema of the function on the given interval, and say where they occur.
-
(Multiple Choice)
4.7/5  (43)
(43)
Solve the problem.
-Given the velocity and initial position of a body moving along a coordinate line at time , find the body's positios .
(Multiple Choice)
4.7/5  (39)
(39)
Find the absolute extreme values of the function on the interval.
-
(Multiple Choice)
4.8/5  (42)
(42)
Use Newton's method to estimate the requested solution of the equation. Start with given value of x0 and then give x2 as
the estimated solution.
-
(Multiple Choice)
4.9/5  (43)
(43)
Find the extreme values of the function and where they occur.
-
(Multiple Choice)
4.8/5  (29)
(29)
Find the value or values of that satisfy the equation in the conclusion of the Mean Value Theorem for the function and interval.
-
(Multiple Choice)
4.9/5  (36)
(36)
Find the largest open interval where the function is changing as requested.
-Decreasing
(Multiple Choice)
4.9/5  (39)
(39)
Showing 61 - 80 of 412
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)