Exam 5: Applications of Derivatives
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
Identify the function's extreme values in the given domain, and say where they are assumed. Tell which of the extreme
values, if any, are absolute.
-
(Multiple Choice)
4.8/5  (40)
(40)
Find the largest open interval where the function is changing as requested.
-Increasing y = 7x - 5
(Multiple Choice)
4.9/5  (41)
(41)
Solve the problem.
-Use Newton's method to estimate the solutions of the equation . Start with for the right-hand solution and with for the solution on the left. Then, in each case find .
(Essay)
5.0/5  (45)
(45)
Identify the function's extreme values in the given domain, and say where they are assumed. Tell which of the extreme
values, if any, are absolute.
-
(Multiple Choice)
4.9/5  (34)
(34)
Determine from the graph whether the function has any absolute extreme values on the interval [a, b].
-![Determine from the graph whether the function has any absolute extreme values on the interval [a, b]. -](https://storage.examlex.com/TB6591/11eb49f8_e010_1761_b71a_6dbe70856432_TB6591_00.jpg)
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-The graphs below show the first and second derivatives of a function . Select a possible graph that passe through the point .
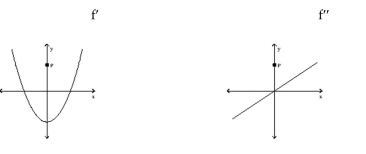
(Multiple Choice)
4.9/5  (44)
(44)
Solve the problem.
-From a thin piece of cardboard 50 in. by ., square corners are cut out so that the sides can be folded up to make a box. What dimensions will yield a box of maximum volume? What is the maximum volume? Round to the nearest tenth, if necessary.
(Multiple Choice)
4.9/5  (45)
(45)
Find the extreme values of the function and where they occur.
-
(Multiple Choice)
4.8/5  (34)
(34)
Find the largest open interval where the function is changing as requested.
-Decreasing
(Multiple Choice)
4.9/5  (30)
(30)
Find the function with the given derivative whose graph passes through the point P.
-
(Multiple Choice)
4.8/5  (40)
(40)
Solve the problem.
-If the price charged for a candy bar is cents, then thousand candy bars will be sold in a certain city, where . How many candy bars must be sold to maximize revenue?
(Multiple Choice)
4.9/5  (32)
(32)
Find the value or values of that satisfy the equation in the conclusion of the Mean Value Theorem for the function and interval.
- Round to the nearest thousandth.
(Multiple Choice)
4.9/5  (31)
(31)
Use a computer algebra system (CAS) to solve the given initial value problem.
-
(Multiple Choice)
4.9/5  (35)
(35)
Answer the problem.
-Consider the quartic function . Must this function have at least one critical point? Give reasons for your answer. (Hint: Must for some ?) How many local extreme values can have?
(Essay)
4.7/5  (40)
(40)
Solve the problem.
-How close does the curve come to the point ? (Hint: If you minimize the square of the distance, you can avoid square roots.)
(Multiple Choice)
4.9/5  (33)
(33)
For the given expression y, find y'' and sketch the general shape of the graph of y = f(x).
-
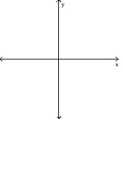
(Multiple Choice)
4.9/5  (37)
(37)
Showing 101 - 120 of 412
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)