Exam 5: Applications of Derivatives
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
Graph the equation. Include the coordinates of any local and absolute extreme points and inflection points.
-
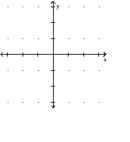
(Multiple Choice)
4.9/5  (35)
(35)
Solve the problem.
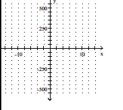
-The graph below shows the position of a body moving back and forth on a coordinate line. (a) When is the body moving away from the origin? Toward the origin? At approximately what times is the (b) velocity equal to zero? (c) Acceleration equal to zero? (d) When is the acceleration positive? Negative?
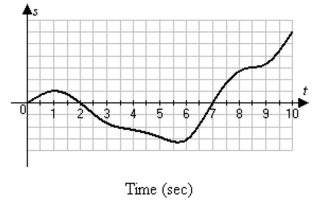 8.5
8.5
(Essay)
4.9/5  (40)
(40)
Graph the equation. Include the coordinates of any local and absolute extreme points and inflection points.
-
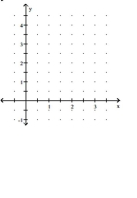
(Multiple Choice)
4.9/5  (36)
(36)
Graph the equation. Include the coordinates of any local and absolute extreme points and inflection points.
-
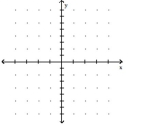
(Multiple Choice)
4.9/5  (33)
(33)
Estimate the limit by graphing the function for an appropriate domain. Confirm your estimate by using L'Hopital's rule.
Show each step of your calculation.
-
(Essay)
4.8/5  (40)
(40)
Determine from the graph whether the function has any absolute extreme values on the interval [a, b].
-![Determine from the graph whether the function has any absolute extreme values on the interval [a, b]. -](https://storage.examlex.com/TB6591/11eb49f8_e010_3e72_b71a_add9ad9f3ede_TB6591_00.jpg)
(Multiple Choice)
4.9/5  (27)
(27)
Sketch the graph and show all local extrema and inflection points.
-
(Multiple Choice)
4.8/5  (44)
(44)
Use differentiation to determine whether the integral formula is correct.
-
(True/False)
4.8/5  (41)
(41)
Find the absolute extreme values of the function on the interval.
-
(Multiple Choice)
4.8/5  (32)
(32)
Find the function with the given derivative whose graph passes through the point P.
-
(Multiple Choice)
4.7/5  (30)
(30)
Using the derivative of f(x) given below, determine the intervals on which f(x) is increasing or decreasing.
-
(Multiple Choice)
4.9/5  (31)
(31)
L'Hopital's rule does not help with the given limit. Find the limit some other way.
-
(Multiple Choice)
4.8/5  (29)
(29)
Find the derivative at each critical point and determine the local extreme values.
-
(Multiple Choice)
4.8/5  (33)
(33)
Solve the problem.
-A small frictionless cart, attached to the wall by a spring, is pulled back from its rest position and released at time to roll back and forth for . Its position at time is
. What is the cart's maximum speed? When is the cart moving that fast? What is the magnitude of of the acceleration then?
(Multiple Choice)
5.0/5  (43)
(43)
Estimate the limit by graphing the function for an appropriate domain. Confirm your estimate by using L'Hopital's rule.
Show each step of your calculation.
-
(Essay)
4.9/5  (48)
(48)
Showing 301 - 320 of 412
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)