Exam 5: Applications of Derivatives
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
Solve the problem.
-Find the number of units that must be produced and sold in order to yield the maximum profit, given the follow equations for revenue and cost:
R(x)=2x G(x)=0.01+0.9x+40
(Multiple Choice)
4.9/5  (35)
(35)
Solve the problem.
-Given the velocity and initial position of a body moving along a coordinate line at time , find the body's position .
(Multiple Choice)
4.9/5  (39)
(39)
Find the extreme values of the function and where they occur.
-
(Multiple Choice)
4.9/5  (41)
(41)
Using the derivative of f(x) given below, determine the intervals on which f(x) is increasing or decreasing.
-
(Multiple Choice)
4.9/5  (37)
(37)
Find the absolute extreme values of the function on the interval.
-
(Multiple Choice)
4.9/5  (36)
(36)
Solve the problem.
-Given the velocity and initial position of a body moving along a coordinate line at time t, find the body's position .
(Multiple Choice)
4.7/5  (47)
(47)
Using the derivative of f(x) given below, determine the critical points of f(x).
-
(Multiple Choice)
4.8/5  (46)
(46)
Solve the problem.
-At noon, ship A was 15 nautical miles due north of ship B. Ship A was sailing south at 15 knots (nautical miles per hour; a nautical mile is 2000 yards) and continued to do so all day. Ship B was sailing east at 6 knots and
Continued to do so all day. The visibility was 5 nautical miles. Did the ships ever sight each other?
(Multiple Choice)
4.8/5  (36)
(36)
Solve the problem.
-Use Newton's method to estimate the one real solution of . Start with and then find
(Essay)
4.9/5  (36)
(36)
Find the function with the given derivative whose graph passes through the point P.
-
(Multiple Choice)
5.0/5  (29)
(29)
Find the largest open interval where the function is changing as requested.
-Decreasing
(Multiple Choice)
4.9/5  (36)
(36)
Solve the problem.
-The 8 ft wall shown here stands 27 feet from the building. Find the length of the shortest straight beam that will reach to the side of the building from the ground outside the wall.
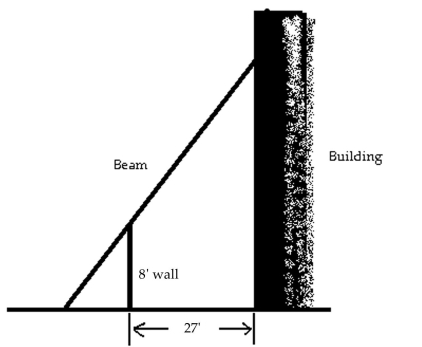
(Multiple Choice)
4.9/5  (43)
(43)
Using the derivative of f(x) given below, determine the intervals on which f(x) is increasing or decreasing.
-
(Multiple Choice)
4.9/5  (39)
(39)
Answer the question.
-It took 29 seconds for the temperature to rise from to when a thermometer was taken from a freezer and placed in boiling water. Although we do not have detailed knowledge about the rate of temperature increase, we can know for certain that, at some time, the temperature was increasing at a rate of .
Explain.
(Essay)
4.7/5  (41)
(41)
Provide an appropriate response.
- is never zero. Does th is example contradict Rolle's Theorem?
(Essay)
4.9/5  (33)
(33)
Showing 221 - 240 of 412
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)