Exam 5: Applications of Derivatives
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
Solve the problem.
-Using the following properties of a twice-differentiable function , select a possible graph of .

(Multiple Choice)
4.8/5  (41)
(41)
Answer each question appropriately.
-Find the standard equation for the position of a body moving with a constant acceleration a along a coordinate The following properties are known:
i. ,
ii. when , and
iii. when ,
where is time, is the initial position, and is the initial velocity.
(Multiple Choice)
4.9/5  (38)
(38)
Solve the problem.
-Suppose the derivative of the function is . At what points, if any, does the graph of have a local minimum or local maximum?
(Multiple Choice)
4.8/5  (38)
(38)
Find the function with the given derivative whose graph passes through the point P.
-
(Multiple Choice)
4.7/5  (38)
(38)
Estimate the limit by graphing the function for an appropriate domain. Confirm your estimate by using L'Hopital's rule.
Show each step of your calculation.
-A student attempted to use l'Hôpital's Rule as follows. Identify the student's error.
= ===1
(Essay)
4.9/5  (43)
(43)
Solve the problem.
-Find the optimum number of batches (to the nearest whole number) of an item that should be produced annually (in order to minimize cost) if 60,000 units are to be made, it costs $4 to store a unit for one year, and it
Costs $600 to set up the factory to produce each batch. Assume that units of this item will be sold off throughout
The year, so the cost equation will use the average cost.
(Multiple Choice)
4.8/5  (36)
(36)
Find the largest open interval where the function is changing as requested.
-Increasing
(Multiple Choice)
4.9/5  (43)
(43)
Provide an appropriate response.
-As moves from left to right though the point , is the graph of rising, or is it falling? Give reasons for your answer.
(Essay)
4.9/5  (47)
(47)
Solve the problem.
-Find the approximate values of through in the factorization
(Essay)
4.8/5  (40)
(40)
Sketch the graph and show all local extrema and inflection points.
-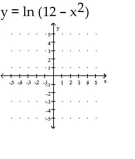
(Multiple Choice)
4.8/5  (31)
(31)
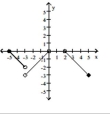
Find the open intervals on which the function is increasing and decreasing. Identify the function's local and absolute extreme values, if any, saying where they occur.
-
(Multiple Choice)
4.9/5  (35)
(35)
Solve the problem.
-Find the table that matches the given graph.
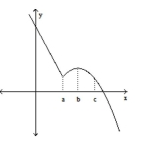
(Multiple Choice)
4.7/5  (39)
(39)
Solve the problem.
-A rectangular sheet of perimeter and dimensions by is to be rolled into a cylinder as shown in part (a) of the figure. What values of and give the largest volume?
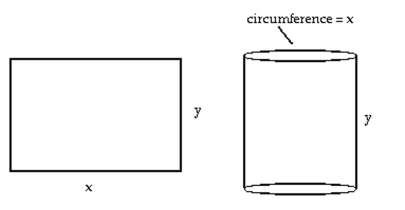
(Multiple Choice)
4.8/5  (33)
(33)
Which of the graphs shows the solution of the given initial value problem?
- when
(Multiple Choice)
5.0/5  (35)
(35)
Showing 81 - 100 of 412
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)