Exam 5: Applications of Derivatives
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
Find the absolute extreme values of the function on the interval.
-
(Multiple Choice)
4.9/5  (35)
(35)
Solve the problem.
-An object is dropped from above the surface of the moon. How long will it take the object to hit the surface of the moon if ?
(Multiple Choice)
4.8/5  (31)
(31)
Answer each question appropriately.
-Suppose the velocity of a body moving along the s-axis is .
Is it necessary to know the initial position of the body to find the body's displacement over some time interval? J your answer. ify
(Multiple Choice)
4.8/5  (45)
(45)
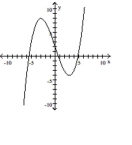
Use the graph of the function f(x) to locate the local extrema and identify the intervals where the function is concave up
and concave down.
-
(Multiple Choice)
4.8/5  (42)
(42)
Identify the function's extreme values in the given domain, and say where they are assumed. Tell which of the extreme
values, if any, are absolute.
-
(Multiple Choice)
4.8/5  (35)
(35)
The function has a non-removable discontinuity at x = 0. The mean value theorem does not apply.
-Let f have a derivative on an interval I. f' has successive distinct zeros at x = 1 and x = 5. Prove that there can be at most one zero of f on the interval (1, 5).
(Essay)
4.9/5  (32)
(32)
Solve the problem.
-The graphs below show the first and second derivatives of a function . Select a possible graph that passe through the point .
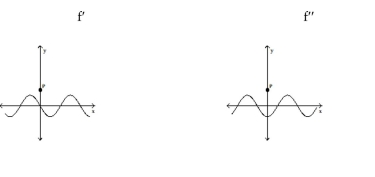
(Multiple Choice)
4.8/5  (45)
(45)
Solve the problem.
-Suppose a business can sell x gadgets for p = 250 - 0.01x dollars apiece, and it costs the business c(x) = 1000 + 25x dollars to produce the x gadgets. Determine the production level and cost per gadget required
To maximize profit.
(Multiple Choice)
4.7/5  (26)
(26)
The function has a non-removable discontinuity at x = 0. The mean value theorem does not apply.
-Suppose that f'(x) = 2x for all x. Find f(8) if f(-2) = 2.
(Multiple Choice)
4.8/5  (35)
(35)
Solve the problem.
-Find the table that matches the graph below.
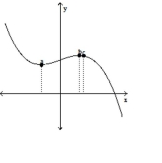
(Multiple Choice)
4.8/5  (34)
(34)
Use the maximum/minimum finder on a graphing calculator to determine the approximate location of all local extrema.
-
(Multiple Choice)
4.8/5  (36)
(36)
Find the largest open interval where the function is changing as requested.
-Decreasing
(Multiple Choice)
4.8/5  (33)
(33)
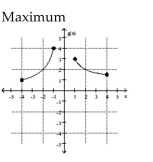
Find the location of the indicated absolute extremum for the function.
-
(Multiple Choice)
4.8/5  (35)
(35)
Find the location of the indicated absolute extremum for the function.
-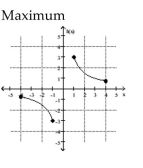
(Multiple Choice)
4.8/5  (41)
(41)
Estimate the limit by graphing the function for an appropriate domain. Confirm your estimate by using L'Hopital's rule.
Show each step of your calculation.
-
(Essay)
4.9/5  (37)
(37)
Solve the problem.
-The graphs below show the first and second derivatives of a function . Select a possible graph of that passes through the point .
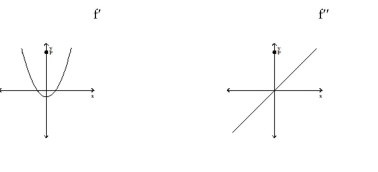
(Multiple Choice)
4.9/5  (27)
(27)
Find the function with the given derivative whose graph passes through the point P.
-
(Multiple Choice)
4.8/5  (42)
(42)
Showing 341 - 360 of 412
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)