Exam 5: Applications of Derivatives
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
For the given expression y, find y'' and sketch the general shape of the graph of y = f(x).
- =
(Multiple Choice)
4.8/5  (39)
(39)
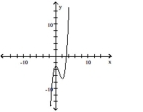
Use the graph of the function f(x) to locate the local extrema and identify the intervals where the function is concave up
and concave down.
-
(Multiple Choice)
4.9/5  (44)
(44)
Solve the problem.
-You are planning to close off a corner of the first quadrant with a line segment 17 units long running from ( ) to . Show that the area of the triangle enclosed by the segment is largest when .
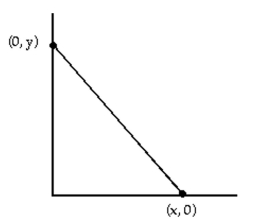
(Essay)
4.8/5  (38)
(38)
Solve the problem.
-Find the number of units that must be produced and sold in order to yield the maximum profit, given the follow equations for revenue and cost:
R(x)=30x-0.5 C(x)=2x+8
(Multiple Choice)
4.8/5  (36)
(36)
Solve the problem.
-The acceleration of gravity near the surface of Mars is . If a rock is blasted straight up from the surface with an initial velocity of (about ), how high does it go? (Hint: When is velocity zero?)
(Multiple Choice)
4.8/5  (49)
(49)
Solve the problem.
-Use Newton's method to estimate the solutions of the equation . Start with for the right-hand solution and with for the solution on the left. Then, in each case find .
(Essay)
5.0/5  (41)
(41)
Use the maximum/minimum finder on a graphing calculator to determine the approximate location of all local extrema.
-
(Multiple Choice)
4.7/5  (39)
(39)
Determine whether the function satisfies the hypotheses of the Mean Value Theorem for the given interval.
-
(True/False)
4.8/5  (34)
(34)
Solve the problem.
-Determine the dimensions of the rectangle of largest area that can be inscribed in a semicircle of radius
(Multiple Choice)
4.7/5  (36)
(36)
Identify the function's local and absolute extreme values, if any, saying where they occur.
-
(Multiple Choice)
4.9/5  (41)
(41)
Identify the function's local and absolute extreme values, if any, saying where they occur.
-
(Multiple Choice)
4.7/5  (40)
(40)
Identify the function's extreme values in the given domain, and say where they are assumed. Tell which of the extreme
values, if any, are absolute.
-
(Multiple Choice)
4.8/5  (28)
(28)
Find the derivative at each critical point and determine the local extreme values.
-
(Multiple Choice)
4.8/5  (34)
(34)
Solve the problem.
-On our moon, the acceleration of gravity is . If a rock is dropped into a crevasse, how fast will it be going just before it hits bottom 45 seconds later?
(Multiple Choice)
4.9/5  (25)
(25)
Find the absolute extreme values of the function on the interval.
-
(Multiple Choice)
4.8/5  (42)
(42)
Estimate the limit by graphing the function for an appropriate domain. Confirm your estimate by using L'Hopital's rule.
Show each step of your calculation.
-Which one is correct, and which one is wrong? Give reasons for your answers.
(a)
(b)
(Essay)
4.8/5  (31)
(31)
Showing 321 - 340 of 412
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)