Exam 8: Infinite Sequences and Series
Exam 1: Functions and Models118 Questions
Exam 2: Limits and Derivatives127 Questions
Exam 3: Differentiation Rules248 Questions
Exam 4: Applications of Differentiation273 Questions
Exam 5: Integrals239 Questions
Exam 6: Applications of Integration189 Questions
Exam 7: Differential Equations154 Questions
Exam 8: Infinite Sequences and Series341 Questions
Exam 9: Vectors and the Geometry of Space269 Questions
Exam 10: Vector Functions111 Questions
Exam 11: Partial Derivatives294 Questions
Exam 12: Multiple Integrals270 Questions
Exam 13: Vector Calculus240 Questions
Select questions type
Find a power series representation for and give its radius of convergence.
(Essay)
4.8/5  (32)
(32)
Construct an example of power series that has as its interval of convergence.
(Essay)
4.8/5  (33)
(33)
Consider the series .(a) Show that the series is absolutely convergent.(b) Calculate the sum of the first 3 terms to approximate the sum of the series.(c) Is the approximation in part (b) an overestimate or an underestimate?
(d) Estimate the error involved in the approximation from part (b).
(Essay)
4.9/5  (34)
(34)
Find a power series representation for the function and determine the radius of convergence.
(Essay)
4.9/5  (39)
(39)
Determine whether the series is convergent or divergent. If it is convergent, find the sum.
(Essay)
4.9/5  (31)
(31)
Determine whether each of the following series is convergent or divergent.(a) (b) (c)
(Short Answer)
4.9/5  (29)
(29)
Determine whether the series is convergent or divergent. If it is convergent, find the sum.
(Short Answer)
4.8/5  (37)
(37)
Use the sum of the first 10 terms to approximate the sum of the series . Estimate the error involved in this approximation.
(Essay)
4.8/5  (41)
(41)
Consider a sequence of rectangles, , , , . . . illustrated in the figure below: 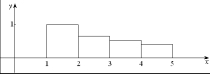 (a) The height of is given by where . Write down the first five terms of and determine the limit of .
(b) Let . Compare to .
(c) Determine whether converges or diverges. Justify your answer.
(a) The height of is given by where . Write down the first five terms of and determine the limit of .
(b) Let . Compare to .
(c) Determine whether converges or diverges. Justify your answer.
(Essay)
4.9/5  (34)
(34)
Construct an example of power series that has as its interval of convergence.
(Essay)
4.8/5  (43)
(43)
Determine if the series converges or diverges by the Ratio Test or Root Test.
(Essay)
4.8/5  (35)
(35)
Showing 201 - 220 of 341
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)