Exam 8: Infinite Sequences and Series

Find the sum of the series $\sum _ { n = 1 } ^ { \infty } \frac { 1 - n ^ { 2 } } { 4 n ^ { 2 } + n + 1 }$ .

A car purchased for $18,000 depreciates 5% each year.(a) If $P _ { n }$ is the value of the car after n years, find a formula for $P _ { n }$ .(b) What does the value of the car approach as time goes on?

Construct an example of power series that has $( 3,5 ]$ as its interval of convergence.

Determine the limit of the sequence $a _ { n } = [ \ln ( n + 1 ) - \ln ( n ) ]$ .

(a) Use series to compute $\int _ { 0 } ^ { 1 } x \cos x d x$ correct to three decimal places.(b) Use integration by parts to compute $\int _ { 0 } ^ { 1 } x \cos x d x$ .(c) Compare your answers in parts (a) and (b) above.

For which of the following series will the Test for Divergence establish divergence? 1) $\sum _ { n = 1 } ^ { \infty } ( - 1 ) ^ { n }$ 2) $\sum _ { n = 1 } ^ { \infty } n ^ { - 1 }$ 3) $\sum _ { n = 1 } ^ { \infty } \frac { n + 1 } { 2 n }$

Find the sum of the series $\sum _ { n = 0 } ^ { \infty } \frac { 1 } { ( 2 n ) ! }$ .

Find the sum of the series $2 + \frac { 1 } { 2 } + \frac { 1 } { 8 } + \frac { 1 } { 32 } + \cdots$ .

Give the 4th-degree Taylor polynomial for $f ( x ) = \sqrt { x }$ about the point $x = 4$ . Using this polynomial, approximate $\sqrt { 4.2 }$ . Give the maximum error for this approximation.

For the series $\sum _ { n - 2 } ^ { \infty } \frac { n ^ { 1 / 2 } } { \ln n }$ , tell whether or not it converges, and indicate what test you used. If the test involves a limit, give the limit. If the test involves a comparison, give the comparison.

Give the Taylor series expansion of $f ( x ) = \sin x$ about the point $c = \frac { \pi } { 4 }$ .

Determine whether $a _ { n } = \frac { 3 n + 4 } { 2 n + 5 }$ is increasing, decreasing, or not monotonic.

Find the third-degree Taylor polynomial of the function $f ( x ) = \int _ { 0 } ^ { x } \sin t ^ { 2 } d t \text { at } a = 0$ .

Consider the recursive sequence defined by $x _ { 1 } = 1 ; x _ { n + 1 } = \frac { x _ { n } ^ { 2 } + 2 } { 2 x _ { n } } , n > 1$ . You may assume the sequence to be monotonic (after the first term) and bounded and hence convergent. Find its limit.

A sequence of right triangles, $A _ { 1 }$ , $A _ { 2 }$ , $A _ { 3 }$ , ... is given in the figure below: 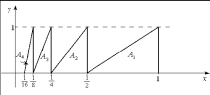(a) Let $a _ { n } = \operatorname { area } \left( A _ { n } \right)$ . Determine an expression for $a _ { n }$ and find the limit of $a _ { n }$ .(b) Let $b _ { n } = \sum _ { k = 1 } ^ { n } a _ { k }$ . Use geometric reasoning to determine the limit of $b _ { n }$ .

Which of the three series below converges? 1) $\sum _ { n = 1 } ^ { \infty } \left( \frac { 2 n - 1 } { 3 n } \right) ^ { n }$ 2) $\sum _ { n = 1 } ^ { \infty } \frac { 1 } { 2 ^ { n } + n }$ 3) $\sum _ { n = 1 } ^ { \infty } \frac { 2 ^ { n } + ( - 3 ) ^ { n } } { 3 ^ { n } }$

Find a power series representation for the function $f ( x ) = \frac { x ^ { 2 } } { 1 - 3 x }$ .

Which of the three series below converges? 1) $\sum _ { n = 1 } ^ { \infty } \left( \frac { 1 } { \sqrt [ 5 ] { n ^ { 4 } } } + \frac { 2 } { n ^ { 3 } } \right)$ 2) $\sum _ { n = 1 } ^ { \infty } \frac { \ln n } { n ^ { 2 } }$ 3) $\sum _ { n = 1 } ^ { \infty } \frac { \sin ( 1 / n ) } { n }$

Consider the recursive sequence defined by $x _ { 1 } = 1 ; x _ { n + 1 } = \frac { x _ { n } ^ { 2 } + 2 } { 2 x _ { n } } , n > 1$ . Evaluate the first three terms of this sequence.

Which of the following is the power series centered at $a = 0$ for $f ( x ) = \frac { 1 } { x ^ { 2 } + 4 }$ ? 1) $\sum _ { n = 0 } ^ { \infty } \frac { ( - 1 ) ^ { n } } { 4 ^ { n + 1 } } x ^ { n }$ 2) $\sum _ { n = 0 } ^ { \infty } \frac { ( - 1 ) ^ { n } } { 4 ^ { n + 1 } } x ^ { 2 n }$ 3) $\sum _ { n = 0 } ^ { \infty } \frac { ( - 1 ) ^ { n } } { 4 ^ { n } } x ^ { 2 n }$