Exam 15: Partial Derivatives
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
Solve the problem.
-What is the distance from the surface to the origin?
(Multiple Choice)
4.8/5  (44)
(44)
Compute the gradient of the function at the given point.
-
(Multiple Choice)
4.8/5  (44)
(44)
Provide an appropriate response.
-For which of the following functions do both and exist?
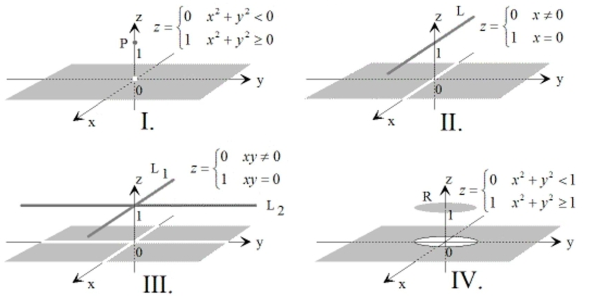
(Multiple Choice)
4.9/5  (32)
(32)
Determine whether the given function satisfies a Laplace equation.
-
(True/False)
4.7/5  (43)
(43)
Solve the problem.
-The surface area of a hollow cylinder (tube) is given by where is the length of the cylinder and and are the outer and inner radii. If , and are measured to be 6 inches, 7 inches, and 9 inches respectively, and if these measurements are accurate to within inches, estimate the maximum percentage error in computing .
(Multiple Choice)
4.7/5  (34)
(34)
Write a chain rule formula for the following derivative.
- for
(Multiple Choice)
4.9/5  (47)
(47)
Use Taylor's formula to find the requested approximation of f(x, y) near the origin.
-Cubic approximation to f(x, y) = ln(1 + 7x + y)
(Multiple Choice)
4.8/5  (46)
(46)
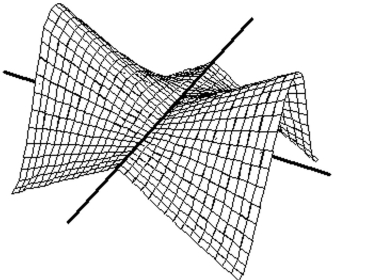
Match the surface show below to the graph of its level curves.
-
(Multiple Choice)
4.8/5  (38)
(38)
Show that the function is a solution of the wave equation.
-w(x, t) = ln cxt
(True/False)
4.8/5  (35)
(35)
Write a chain rule formula for the following derivative.
-
(Multiple Choice)
4.9/5  (31)
(31)
Write a chain rule formula for the following derivative.
- for
(Multiple Choice)
4.8/5  (37)
(37)
Find the derivative of the function at P0 in the direction of u.
-
(Multiple Choice)
4.8/5  (36)
(36)
At what points is the given function continuous?
-f(x, y, z) = ln(x + y + z - 6)
(Multiple Choice)
4.8/5  (43)
(43)
Solve the problem.
-A rectangle with sides parallel to the axes is inscribed in the region bounded by the axes and the line x + 2y = 2. Find the maximum area of this rectangle.
(Multiple Choice)
4.8/5  (40)
(40)
Showing 181 - 200 of 409
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)