Exam 15: Partial Derivatives
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
Find the absolute maxima and minima of the function on the given domain.
-f(x, y) = 4x + 3y on the trapezoidal region with vertices (0, 0), (1, 0), (0, 2), and (1, 1)
(Multiple Choice)
4.9/5  (43)
(43)
Solve the problem.
-The resistance produced by wiring resistors of , and ohms in parallel can be calculated from the formula
If , and are measured to be 4 ohms, 7 ohms, and 9 ohms respectively, and if these measurements are accurate to within ohms, estimate the maximum percentage error in computing R.
(Multiple Choice)
5.0/5  (44)
(44)
Solve the problem.
-The table below summarizes the construction cost of a set of homes (excluding the lot cost) along with the square footage of the home's floor space. Find a linear equation that relates the construction cost in thousands of dollars to the floor space in hundreds of square feet by finding the least squares line for the data.
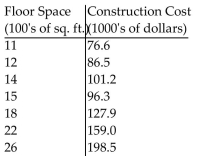
(Multiple Choice)
4.8/5  (31)
(31)
Solve the problem.
-Write an equation for the tangent line to the curve xy = 40 at the point (8, 5).
(Multiple Choice)
4.8/5  (36)
(36)
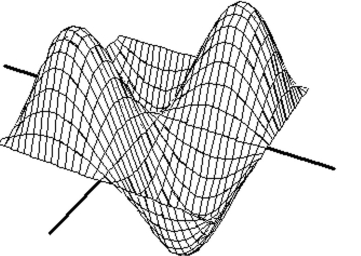
Match the surface show below to the graph of its level curves.
-
(Multiple Choice)
4.7/5  (45)
(45)
Find two paths of approach from which one can conclude that the function has no limit as (x, y) approaches (0, 0).
-If and the limit of exists as approaches , what can you say about the continuity of at the point ? Give reasons for your answer.
(Essay)
4.8/5  (40)
(40)
Use Taylor's formula to find the requested approximation of f(x, y) near the origin.
-Quadratic approximation to f(x, y) = sin(10x + y)
(Multiple Choice)
4.8/5  (41)
(41)
Answer the question.
-Describe the results of applying the method of Lagrange multipliers to a function f(x, y) if the points (x, y) are constrained to follow a curve g(x, y) = c that is everywhere perpendicular to the level curves of f. Assume that
Both f(x, y) and g(x, y) satisfy all the requirements and conditions for the method to be applicable.
(Multiple Choice)
4.8/5  (30)
(30)
Use polar coordinates to find the limit of the function as (x, y) approaches (0, 0).
-
(Multiple Choice)
4.8/5  (40)
(40)
Match the surface show below to the graph of its level curves.
-
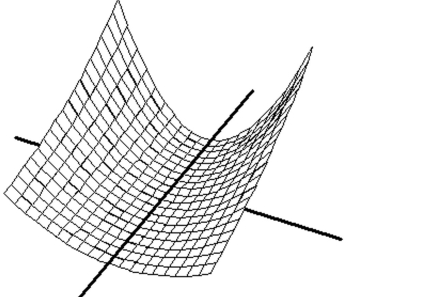
(Multiple Choice)
4.8/5  (41)
(41)
Find two paths of approach from which one can conclude that the function has no limit as (x, y) approaches (0, 0).
-
(Essay)
4.9/5  (31)
(31)
Find an upper bound for the magnitude |E| of the error in the approximation f(x, y) ≈ L(x, y) at the given point over the
given region R.
-
(Multiple Choice)
4.9/5  (43)
(43)
Use polar coordinates to find the limit of the function as (x, y) approaches (0, 0).
-
(Multiple Choice)
4.8/5  (34)
(34)
Solve the problem.
-Find the distance between the skew lines x = t - 6, y = t, z = 2t And X = t, y = t, z = -t.
(Multiple Choice)
4.9/5  (42)
(42)
Find the equation for the level surface of the function through the given point.
-
(Multiple Choice)
4.8/5  (39)
(39)
Solve the problem.
-The radius r and height h of a cylinder are changing with time. At the instant in question, r = 2 cm, h = 6 cm, dr/dt = 0.03 cm/sec and dh/dt = -0.03 cm/sec. At what rate is the cylinder's volume changing at that instant?
(Multiple Choice)
4.8/5  (37)
(37)
Find all the second order partial derivatives of the given function.
-
(Multiple Choice)
4.8/5  (49)
(49)
Showing 281 - 300 of 409
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)