Exam 15: Partial Derivatives
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
Find an upper bound for the magnitude |E| of the error in the approximation f(x, y) ≈ L(x, y) at the given point over the
given region R.
- at
(Multiple Choice)
4.9/5  (44)
(44)
Use the limit definition of the partial derivative to compute the indicated partial derivative of the function at the specified point.
-
(Essay)
4.9/5  (38)
(38)
Use the limit definition of the partial derivative to compute the indicated partial derivative of the function at the specified point.
-
(Essay)
4.8/5  (41)
(41)
Find the derivative of the function at P0 in the direction of u.
-
(Multiple Choice)
5.0/5  (43)
(43)
Provide an appropriate response.
-Which order of differentiation will calculate faster, first or first?
(Multiple Choice)
4.8/5  (34)
(34)
Answer the question.
-The graph below shows the level curves of a differentiable function (thin curves) as well as the constraint (thick circle). Using the concepts of the orthogonal gradient theorem and the method of Lagrange multipliers, estimate the coordinates corresponding to the constrained extrema of .
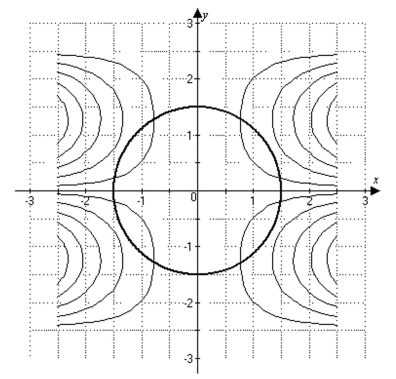
(Multiple Choice)
4.8/5  (33)
(33)
Find two paths of approach from which one can conclude that the function has no limit as (x, y) approaches (0, 0).
-
(Essay)
4.8/5  (36)
(36)
Find the extreme values of the function subject to the given constraint.
-
(Multiple Choice)
4.7/5  (33)
(33)
Find the absolute maxima and minima of the function on the given domain.
-
(Multiple Choice)
5.0/5  (39)
(39)
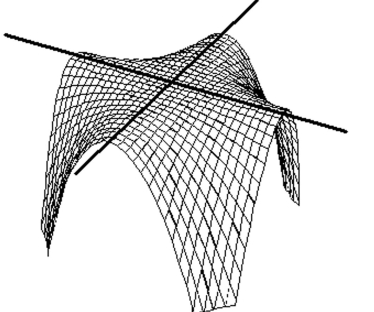
Match the surface show below to the graph of its level curves.
-
(Multiple Choice)
4.8/5  (38)
(38)
Solve the problem.
-Write an equation for the tangent line to the curve at the point .
(Multiple Choice)
4.8/5  (38)
(38)
Use Taylor's formula to find the requested approximation of f(x, y) near the origin.
-Quadratic approximation to
(Multiple Choice)
4.8/5  (42)
(42)
Find the extreme values of the function subject to the given constraint.
-
(Multiple Choice)
4.8/5  (37)
(37)
Showing 221 - 240 of 409
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)