Exam 15: Partial Derivatives

Find an upper bound for the magnitude |E| of the error in the approximation f(x, y) ≈ L(x, y) at the given point over the given region R. - $f ( x , y ) = - 4 x ^ { 2 } + 9 y ^ { 2 } - 9 \text { at } ( - 3 , - 2 ) ; R : | x + 3 | \leq 0.1 , | y + 2 | \leq 0.1$

Write a chain rule formula for the following derivative. - $\frac { \partial \mathrm { w } } { \partial \mathrm { t } } \text { for } \mathrm { w } = \mathrm { f } ( \mathrm { p } , \mathrm { q } , \mathrm { r } ) ; \mathrm { p } = \mathrm { g } ( \mathrm { t } ) , \mathrm { q } = \mathrm { h } ( \mathrm { t } ) , \mathrm { r } = \mathrm { k } ( \mathrm { t } )$

Find two paths of approach from which one can conclude that the function has no limit as (x, y) approaches (0, 0). - $f ( x , y ) = \frac { x y } { x ^ { 2 } + y ^ { 2 } }$

Find the extreme values of the function subject to the given constraint. - $f ( x , y , z ) = 4 x - 3 y + 2 z , \quad x ^ { 2 } + y ^ { 2 } = 6 z$

Provide an appropriate answer. -Suppose that $x ^ { 2 } + y ^ { 2 } = r ^ { 2 }$ and $x = r \cos \theta$ , as in polar coordinates. Find $\left( \frac { \partial y } { \partial \theta } \right) _ { r }$ .

Give an appropriate answer. - $f ( x , y ) = \frac { e ^ { - x } } { x ^ { 2 } + y ^ { 2 } }$

Find the limit. - $\lim _ { ( x , y ) \rightarrow ( 4,3 ) } x \ln y$

At what points is the given function continuous? - $f ( x , y ) = \frac { x y } { x + y }$

Use implicit differentiation to find the specified derivative at the given point. -Find $\frac { \partial y } { \partial z }$ at the point $( 2,3,3 )$ for $\frac { 2 } { x ^ { 2 } } + \frac { 2 } { y ^ { 2 } } + \frac { 4 } { z ^ { 2 } } = 0$ .

Sketch a typical level surface for the function. - $f ( x , y , z ) = \sqrt { x ^ { 2 } - z }$

Find the absolute maximum and minimum values of the function on the given curve. -Function: $f ( x , y ) = x y ;$ curve: $\frac { x ^ { 2 } } { 36 } + \frac { y ^ { 2 } } { 81 } = 1 , y \geq 0$ . (Use the parametric equations $x = 6 \cos t , y = 9 \sin t$ .)

Compute the gradient of the function at the given point. - $f ( x , y ) = - 4 x ^ { 2 } + 6 y , \quad ( 4,3 )$

Sketch the surface z = f(x,y). - $f ( x , y ) = \sqrt { 4 - x ^ { 2 } - y ^ { 2 } }$

Find the extreme values of the function subject to the given constraint. - $f ( x , y ) = 3 x - y + 1 , \quad 3 x ^ { 2 } + y ^ { 2 } = 9$

Find the domain and range and describe the level curves for the function f(x,y). - $f ( x , y ) = \sin ^ { - 1 } \left( x ^ { 2 } + y ^ { 2 } \right)$

Find the specific function value. -Find f(-3, 6) when f(x, y) = 5x + 2y - 3.

Find all the second order partial derivatives of the given function. - $f ( x , y ) = \ln \left( x ^ { 2 } y - x \right)$

Find the domain and range and describe the level curves for the function f(x,y). - $f ( x , y ) = 4 x ^ { 2 } - 2 y ^ { 2 }$

Solve the problem. -Find the least squares line for the points (-5, -1), (3, -2).

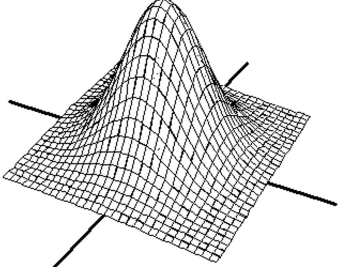
Match the surface show below to the graph of its level curves. -