Exam 15: Partial Derivatives

Solve the problem. -The Redlich-Kwong equation provides an approximate model for the behavior of real gases. The equation is $\mathrm { P } ( \mathrm { V } , \mathrm { T } ) = \frac { \mathrm { RT } } { \mathrm { V } - \mathrm { b } } - \frac { \mathrm { a } } { \mathrm { T } ^ { 1 / 2 } \mathrm {~V} ( \mathrm {~V} + \mathrm { b } ) }$ , where $\mathrm { P }$ is pressure, $\mathrm { V }$ is volume, $\mathrm { T }$ is Kelvin temperature, and $a , b$ , and $\mathrm { R }$ are constants. Find the partial derivative of the function with respect to each variable.

Give an appropriate answer. -Given the function $\mathrm { f } ( \mathrm { x } , \mathrm { y } , \mathrm { z } )$ and the positive number $\varepsilon$ as in the formal definition of a limit, find a positive number $\delta$ as in the definition that insures $| f ( x , y , z ) - f ( 0,0,0 ) | < \varepsilon$ . $f ( x , y , z ) = x + y + z ; \varepsilon = 0.12$

Solve the problem. -Find the least squares line for the points (6, 30), (7, -35), (8, 40), (9, -45).

Find the absolute maxima and minima of the function on the given domain. - $f ( x , y ) = x ^ { 2 } + 12 x + y ^ { 2 } + 16 y + 10 \text { on the rectangular region } - 1 \leq x \leq 1 , - 2 \leq y \leq 2$

Find two paths of approach from which one can conclude that the function has no limit as (x, y) approaches (0, 0). - $f ( x , y ) = \frac { y ^ { 2 } } { y ^ { 2 } - x }$

$\text { Find } \mathrm { f } _ { \mathbf { x } } , \mathrm { f } _ { \mathbf { y } } \text {, and } \mathrm { f } _ { \mathbf { Z } }$ - $f ( x , y , z ) = \frac { z } { \sqrt { x + y ^ { 2 } } }$

Find the extreme values of the function subject to the given constraint. - $f ( x , y , z ) = x + y + z , \frac { 1 } { x } + \frac { 1 } { y } + \frac { 1 } { z } = 1$

Find the limit. -

Use implicit differentiation to find the specified derivative at the given point. -Find $\frac { \partial x } { \partial y }$ at the point $\left( 1 , \frac { \pi } { 24 } , 6 \right)$ for $\mathrm { e } ^ { \mathrm { x } ^ { 2 } } \cos \mathrm { yz } = 0$ .

Provide an appropriate response. -Find any local extrema (maxima, minima, or saddle points) of $f ( x , y )$ given that $f _ { X } = 49 x ^ { 2 } - 49$ and $f _ { y } = 3 y + 6$

Solve the problem. -About how much will $f ( x , y ) = \tan ^ { - 1 } x y$ change if the point $( x , y , z )$ moves from $\left( 9 \sqrt { 2 } , \frac { - 6 } { \sqrt { 2 } } \right)$ a distance of $\mathrm { ds } = \frac { 1 } { 10 }$ unit in the direction of $\mathbf { i } + \mathbf { j } ?$

Find all the local maxima, local minima, and saddle points of the function. - $f ( x , y ) = 81 x ^ { 2 } + 72 x y + 64 y ^ { 2 }$

Solve the problem. - $\text { Evaluate } \frac { \partial \mathrm { u } } { \partial \mathrm { z } } \text { at } ( \mathrm { x } , \mathrm { y } , \mathrm { z } ) = ( 3,4,1 ) \text { for the function } \mathrm { u } = \mathrm { p } ^ { 2 } \mathrm { q } ^ { 2 } - \mathrm { r } ; \mathrm { p } = \mathrm { y } - \mathrm { z } , \mathrm { q } = \mathrm { x } + \mathrm { z } , \mathrm { r } = \mathrm { x } + \mathrm { y }$

Find the requested partial derivative. - $( \partial z / \partial x ) _ { y }$ at $( x , y , z ) = ( 1,1,1 )$ if $z ^ { 3 } + 6 x y z = 7$

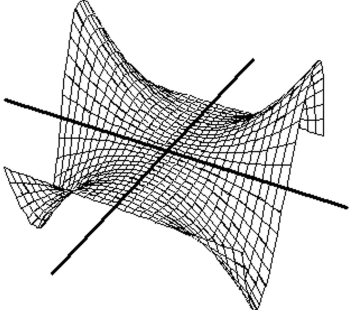
Match the surface show below to the graph of its level curves. -

Solve the problem. -A rectangular box with square base and no top is to have a volume of $32 \mathrm { ft } ^ { 3 }$ . What is the least amount of material required?

Solve the problem. - $\text { Maximize } f ( x , y , z ) = e ^ { 4 x + 9 y + 2 z } \text { subject to } x + y + z = 0 , x + 2 y + 3 z = 0 \text {, and } x + 4 y + 9 z = 0$

Find the specific function value. -Find $f ( 3,6 )$ when $f ( x , y ) = \sqrt { 3 x + y ^ { 2 } }$ .

Provide an appropriate response. -For the space curve $x = t , y = t ^ { 2 } , z = t$ , find the points at which the function $f ( x , y )$ takes on extreme values if $f _ { X } =$ $9 , \mathrm { f } _ { \mathrm { y } } = \frac { \mathrm { t } } { 2 }$ , and $\mathrm { f } _ { \mathrm { z } } = - 30 \mathrm { t }$

Give an appropriate answer. -Given the function $f ( x , y )$ and the positive number $\varepsilon$ as in the formal definition of a limit, find a positive number $\delta$ as in the definition that insures $| \mathrm { f } ( \mathrm { x } , \mathrm { y } ) - \mathrm { f } ( 0,0 ) | < \varepsilon$ . $f ( x , y ) = \frac { x + y } { x ^ { 2 } + y ^ { 2 } + 1 } ; \varepsilon = 0.06$