Exam 15: Partial Derivatives
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
Solve the problem.
-A simple electrical circuit consists of a resistor connected between the terminals of a battery. The voltage (in volts) is dropping as the battery wears out. At the same time, the resistance (in ohms) is increasing as the resistor heats up. The power (in watts) dissipated by the circuit is given by . Use the equation
to find how much the power is changing at the instant when ohms, volts, ohms/sec and , volts/sec.
(Multiple Choice)
4.8/5  (41)
(41)
Solve the problem.
-Amarillo Motors manufactures an economy car called the Citrus, which is notorious for its inability to hold a respectable resale value. The average resale value of a set of 1998 Amarillo Citrus's is summarized in the table below along with the age of the car at the time of resale and the number of cars included in the average. Fit a line of the form to the data, where is the resale value in thousands of dollars and a is the age of the car in years..
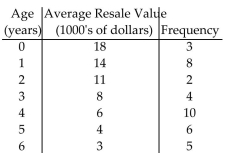
(Multiple Choice)
4.9/5  (43)
(43)
Provide an appropriate response.
-Find the direction in which the function is increasing most rapidly at the point .
(Multiple Choice)
4.9/5  (40)
(40)
Find the extreme values of the function subject to the given constraint.
-
(Multiple Choice)
4.8/5  (43)
(43)
Use the limit definition of the partial derivative to compute the indicated partial derivative of the function at the specified point.
-
(Essay)
4.8/5  (32)
(32)
Find the extreme values of the function subject to the given constraint.
-
(Multiple Choice)
5.0/5  (45)
(45)
Find the domain and range and describe the level curves for the function f(x,y).
-
(Multiple Choice)
4.8/5  (42)
(42)
Use Taylor's formula to find the requested approximation of f(x, y) near the origin.
-Cubic approximation to
(Multiple Choice)
4.9/5  (31)
(31)
Solve the problem.
-Find the least squares line through the points (1, 18), (2, 42), and (3, 36).
(Multiple Choice)
4.8/5  (29)
(29)
Solve the problem.
-Find the points on the curve that are closest to the origin.
(Multiple Choice)
4.7/5  (34)
(34)
Find the absolute maximum and minimum values of the function on the given curve.
-Function: curve: . (Use the parametric equations cos .)
(Multiple Choice)
4.8/5  (31)
(31)
Find an upper bound for the magnitude |E| of the error in the approximation f(x, y) ≈ L(x, y) at the given point over the
given region R.
-
(Multiple Choice)
4.9/5  (32)
(32)
Find the extreme values of the function subject to the given constraint.
-
(Multiple Choice)
5.0/5  (42)
(42)
Find two paths of approach from which one can conclude that the function has no limit as (x, y) approaches (0, 0).
-Does knowing that tell you anything about ? Give reasons for your answer.
(Essay)
4.9/5  (37)
(37)
Find the specific function value.
-Find f(100, 3) when f(x, y) = y log x.
(Multiple Choice)
4.8/5  (33)
(33)
Showing 321 - 340 of 409
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)