Exam 15: Partial Derivatives

Solve the problem. -Find the derivative of the function $f ( x , y , z ) = \frac { x } { y } + \frac { y } { z } + \frac { z } { x }$ at the point $( 7 , - 7,7 )$ in the direction in which the function decreases most rapidly.

Give an appropriate answer. -Given the function $f ( x , y )$ and the positive number $\varepsilon$ as in the formal definition of a limit, find a positive number $\delta$ as in the definition that insures $| \mathrm { f } ( \mathrm { x } , \mathrm { y } ) - \mathrm { f } ( 0,0 ) | < \varepsilon$ . $f ( x , y ) = ( 1 + \cos x ) ( x + y ) ; \varepsilon = 0.08$

Find the derivative of the function at P0 in the direction of u. - $f ( x , y ) = 6 x - 7 y , \quad P _ { 0 } ( - 7 , - 2 ) , \quad u = 4 i - 3 j$

Provide an appropriate response. -Find the direction in which the function is increasing most rapidly at the point $\mathrm { P } _ { 0 }$ . $f ( x , y ) = x e ^ { y } - \ln ( x ) , P _ { 0 } ( - 3,0 )$

Find two paths of approach from which one can conclude that the function has no limit as (x, y) approaches (0, 0). -Does knowing that $\left| \cos \left( \frac { 1 } { y } \right) \right| \leq 1$ tell you anything about $( x , y ) \rightarrow ( 0,0 ) \sin ( x ) \cos \left( \frac { 1 } { y } \right)$ ? Give reasons for your answer.

Solve the problem. -Find the extreme values of $f ( x , y , z ) = 2 x - 3 y + z$ subject to $x ^ { 2 } + y ^ { 2 } = 1$ and $y ^ { 2 } + z ^ { 2 } = 1$ .

Sketch a typical level surface for the function. - $f ( x , y , z ) = 9 e ^ { 6 \left( y ^ { 2 } + z ^ { 2 } \right) }$

Solve the problem. -Find the least squares line for the points (1, 1), (2, 4), (3, 9), (4, 16).

Solve the problem. -Evaluate $\frac { d w } { d t }$ at $t = 6$ for the function $w = e ^ { x y z } z ^ { 2 } ; x = t , y = t , z = \frac { 1 } { t }$ .

Find the domain and range and describe the level curves for the function f(x,y). - $f ( x , y ) = \frac { 1 } { 4 x ^ { 2 } + 5 y ^ { 2 } }$

Solve the problem. -The Van der Waals equation provides an approximate model for the behavior of real gases. The equation is $\mathrm { P } ( \mathrm { V }$ , $\mathrm { T } ) = \frac { \mathrm { RT } } { \mathrm { V } - \mathrm { b } } - \frac { \mathrm { a } } { \mathrm { V } ^ { 2 } }$ , where $\mathrm { P }$ is pressure, $\mathrm { V }$ is volume, $\mathrm { T }$ is Kelvin temperature, and $\mathrm { a } , \mathrm { b }$ , and $\mathrm { R }$ are constants. Find the partial derivative of the function with respect to each variable.

Give an appropriate answer. -Given the function $\mathrm { f } ( \mathrm { x } , \mathrm { y } )$ and the positive number $\varepsilon$ as in the formal definition of a limit, find a positive number $\delta$ as in the definition that insures $| f ( x , y ) - f ( 0,0 ) | < \varepsilon$ . $f ( x , y ) = \frac { 2 x + y } { x ^ { 2 } y ^ { 2 } + 1 } ; \varepsilon = 0.12$

Solve the problem. - $\text { Find parametric equations for the normal line to the surface } z = \ln \left( 7 x ^ { 2 } + 4 y ^ { 2 } + 1 \right) \text { at the point } ( 0,0,0 ) \text {. }$

Find the extreme values of the function subject to the given constraint. - $f ( x , y ) = 4 x + 6 y , x ^ { 2 } + y ^ { 2 } = 13$

Sketch the surface z = f(x,y). - $f ( x , y ) = | x + y |$

Use the limit definition of the partial derivative to compute the indicated partial derivative of the function at the specified point. - $\text { Find } \frac { \partial f } { \partial x } \text { at the point } ( 9 , - 6 , - 6 ) : f ( x , y , z ) = 6 x ^ { 2 } y + 3 y ^ { 2 } + 6 z$

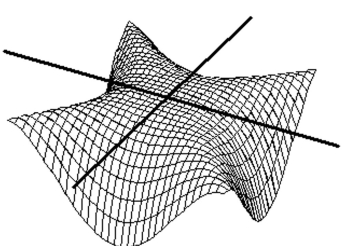
Match the surface show below to the graph of its level curves. -

Provide an appropriate answer. -Find $\frac { \partial z } { \partial v }$ when $u = 0$ and $v = \frac { 11 \pi } { 2 }$ if $z ( x , y ) = \sin x + \cos y , x = u \cdot v$ , and $y = u + v$ .

Solve the problem. -Write parametric equations for the tangent line to the curve of intersection of the surfaces x + y + z = 2 and x - y + 2z = -3 at the point (1, 2, -1).

Estimate the error in the quadratic approximation of the given function at the origin over the given region. - $f ( x , y ) = e ^ { 4 x } \sin y , | x | \leq 0.1 , | y | \leq 0.1$